Chinese Journal of Information Fusion
ISSN: 2998-3371 (Online) | ISSN: 2998-3363 (Print)
Email: [email protected]


Knowledge Graphs (KGs) serve as a foundational tool for information fusion, providing a structured representation of knowledge that facilitates data integration and semantic modeling. However, during the construction of KGs, the occurrence of missing facts, resulting from incomplete, inconsistent, or dynamically evolving data, limits their practical applicability. To address this issue, knowledge reasoning, as a core task in knowledge graph research, aims to complete missing facts based on existing ones. Embedded-based reasoning method is one of the mainstream [1]. This method captures semantic information [2] and reasoning out missing facts by learning low dimensional vector representations of entities and relationships in KGs and utilizing the relative positions and geometric structures between these embedded vectors. Embedding-based reasoning methods are computationally simple, efficient, and suitable for various applications. However, their representational capacity is limited, making it challenging to reason about complex relationships between entities. For complex reasoning tasks, path-based reasoning methods can effectively capture and model multi-level relationship structures and search for multi-hop paths between entities in the KG, using structural information to reason about missing facts and complete the KG. The path-based reasoning method can effectively handle complex relational reasoning tasks [3], but the path search and matching process usually requires traversing a large number of graph structures, resulting in high computational complexity and significantly increasing the consumption of computing resources. Reducing the number of model parameters can decrease computational complexity, enhance reasoning efficiency, and reduce computational costs.
Traditional methods, while reducing the number of parameters to some extent, still face a trade-off between model performance and computational efficiency. As an emerging computing paradigm, quantum circuit, with their unique quantum advantages, can significantly reduce the number of model training parameters while maintaining or improving model performance, thereby further optimizing computational efficiency and reasoning effectiveness. Arute et al. [7] used a quantum processor called Sycamore to perform an extremely difficult random number generation task and compared it with traditional supercomputers. The experimental results indicate that the time required for Sycamore to complete the task is much shorter than that of classical computers, demonstrating the computational advantage of quantum computers over traditional computers in specific tasks. With the deepening of quantum computing research, variational quantum circuit (VQC) have emerged [8]. This method draws on the principles and structures of artificial neural networks, enabling quantum computing to be effectively applied to machine learning tasks. Chen et al. [10] demonstrated that the parameter space complexity of VQC is , while that of the traditional neural network DON is . For KGs, which involve large state and action spaces, VQC can greatly reduce model parameters and computational complexity.
In order to address the challenges of computational complexity and resource consumption in knowledge reasoning models, this paper proposes quantum-inspired reinforcement learning (QIRL), which trains a reinforcement learning strategy network based on quantum circuit and searches for reasoning paths in KGs. Specifically, this paper proposes an embedding-based approach to map the state information of the knowledge graph (KG) into a continuous vector space. This representation is then quantum encoded and input into a strategy network based on quantum circuits for training. Ultimately, the network outputs the probability distribution for the next action. The strategy network based on quantum circuit gradually expands the reasoning path until all reasoning paths in the KG are found. QIRL utilizes the parallelism and entanglement properties of quantum computing, greatly reducing the number of model training parameters, lowering computational complexity, and reducing computational resource consumption. The main contributions of this paper are as follows:
This article proposes a knowledge reasoning model based on quantum circuit training reinforcement learning strategy network for the first time, which uses known facts to supervise the training of quantum circuit, update its parameters, and perform knowledge reasoning;
This article utilizes the parallelism and entanglement properties of quantum computing to reduce computational complexity, The experimental results show that the QIRL method proposed in this paper can significantly reduce the number of model training parameters.
The embedding-based reasoning methods map entities and relationships in KGs to a low dimensional vector space, allowing their semantic and structural information to be expressed in the form of geometric relationships, thereby efficiently handling reasoning tasks in large-scale KGs. Early methods such as TransE [11], TransH [12] and DistlMult [13] focused on studying geometric relationships such as translation, projection, and linear transformation between embedded vectors of entities and relationships, providing efficient and semantic knowledge representation for knowledge reasoning. Lu et al. [14] proposed the DensE method, which decomposes each relationship into rotation and scaling operators in three-dimensional Euclidean space, which can better represent composite relationships. Pavlovic et al. [15] proposed the ExpressivE method, which uses the spatial relationships of super parallel quadrilaterals to represent the semantic structural information between entities and relationships, providing intuitive geometric explanations for knowledge reasoning tasks. Although embedding based reasoning methods have shown good performance in large-scale KGs reasoning tasks, they are difficult to handle relationships with multi-level semantics or nonlinear structures, and have weak modeling capabilities for complex relationships.
The path-based reasoning methods utilizes the powerful expressive power of neural networks to optimize the reasoning process, which can effectively handle reasoning tasks in large-scale KGs. Dettmers et al. [16] proposed a multi-layer convolutional network mode called ConvE for link prediction, which captures the relationship information between entities through convolutional networks and effectively reasons over large-scale KGs. Yang et al. [17] proposed the hyper relation aware multi-view model HyRel, which learns the globally transferable structure of a graph to reason about unseen graphs, offering high flexibility and usability. Xiong et al. [18] proposed a reinforcement learning framework for learning multi-hop relational paths, which effectively handles complex reasoning tasks with ambiguous answers and scales to large KGs. The path-based reasoning methods perform well in large-scale KG reasoning, but the model requires a large number of training parameters, high computational complexity, and demand significant computing and storage resources.
The superposition and entanglement properties of quantum computing give it unique advantages in solving certain computational tasks that traditional computers do not have. Chen et al. [10] explored the potential of quantum computing to enhance reinforcement learning and demonstrated the potential of quantum algorithms in improving time and space complexity in simple environments. Chen et al. [4] proposed the asynchronous training of advantage actor-critic variational quantum policies, which reduces the training time of quantum reinforcement learning. As the application of quantum computing in reinforcement learning progresses, quantum reinforcement learning has been extensively explored and applied across various fields. Kim et al. [5] integrated quantum reinforcement learning into reusable rocket control systems, enhancing both computational efficiency and model stability. Ansere et al. [6] proposed a Quantum-empowered Deep Reinforcement Learning (Qe-DRL) approach to enhance computational learning speed and task processing efficiency for IoT devices under quantum uncertainty and time-varying channel conditions. In addition, quantum reinforcement learning is widely used in fields such as biochemistry and medicine, and has shown good performance. However, the above application scenarios are generally relatively simple, usually requiring only a limited number of qubits and small state and action spaces. KGs typically contain large states and action spaces. To reduce the computational complexity of reasoning models in large-scale KGs, this paper proposes a quantum reinforcement learning based knowledge reasoning model QIRL, which greatly reduces the training parameters of the model by utilizing quantum advantages. The performance of the proposed model is validated on universal datasets. In contrast to emerging LLM-based reasoning methods [9], our approach emphasizes computational efficiency and parameter reduction via quantum-inspired techniques.
A KG contains a large amount of entity and relational data. Given a graph , represents the set of entities and represents the set of relationships between entities. is the set of triplets in a KG, each triplet consisting of a head entity , a relationship , and a tail entity . Due to incomplete data sources and insufficient information extraction, KGs often have missing elements, which can be filled in through knowledge reasoning. According to the type of missing elements, knowledge reasoning tasks can be divided into head reasoning , tail reasoning and relational reasoning , among which indicates missing elements. The path-based knowledge reasoning methods reason about missing facts by searching for paths between entities. As the number of entities and relationships in the KG increases, the number of possible reasoning paths increases exponentially, which makes a comprehensive analysis of these paths computationally complex. Therefore, how to reduce computational complexity while ensuring reasoning accuracy has become a key challenge in current research.
To address the above issues, this paper proposes a quantum reinforcement learning-based knowledge reasoning method, QIRL, which utilizes quantum circuits to train the strategy network and reduce the computational complexity of the training process. The QIRL method consists of two main components: the external environment and the quantum strategy network. The quantum strategy network is primarily composed of quantum circuits, which in turn consist of quantum bits, quantum gates, and measurement operations [5]. Quantum bits are the fundamental units used to construct quantum circuits, while quantum gates serve as the basic units for manipulating quantum bits. Quantum gates perform linear transformations on the states of quantum bits, create entanglement between them, and enable parallelism in quantum computation. This allows quantum circuits to simultaneously process data from multiple quantum bits, significantly reducing the number of model training parameters and lowering computational complexity. After the quantum circuit processes the data of quantum bits in parallel, a measurement is performed on these quantum bits to obtain the output of the quantum strategy network. The quantum strategy network generates the next action based on the current external environment state and continuously updates its parameters until the reasoning process is completed. This paper mainly focuses on tail reasoning tasks, while the other two types of reasoning tasks can be similarly transformed into the form of tail reasoning tasks.
In this section, an overview of the proposed QIRL method is first introduced. The QIRL method trains a reinforcement learning strategy network based on quantum circuit and continuously updates the quantum circuit parameters according to the state of the agent. Afterwards, the training and reasoning process of the QIRL method were described in detail.
The QIRL method updates the parameters of the quantum policy network by continuously interacting with the environment to find the optimal reasoning paths. In this paper, the environment is modeled as a Markov Decision Process (MDP) and the interaction dynamics between the agent and the KG are specified. MDP can be represented by tuple , where represents the continuous state space of the KG as input to the quantum policy network. represents the set of relationships in the KG, that is, the set of all next optional actions output by the quantum policy network. is a state transition probability function that represents the probability of the QIRL policy network transitioning from state to state upon selecting action . is the reward function for each pair , designed to encourage the agent to learn the optimal strategy. The specific settings of the QIRL method are as follows:
Actions: The actions of the quantum policy network can be represented by the relationship in the KG. For the entity pair , starting from the head entity , the agent selects the action with the highest probability as the next action based on the output action probability distribution of the quantum policy network, to extend the path until reaching the real tail entity ; To ensure the consistency of the output dimension of the strategy network, this paper defines the action space as all relationships and their inverse relationships in the KG, and the dimension of the action space is consistent with the number of quantum bits in the quantum circuit.
States: KGs contain a large number of entities and relationships, which are discrete symbols, while policy network training needs to be conducted in a continuous space. In order for the policy network to better capture semantic information, it is necessary to transform entities and relationships into continuous vectors. This model employs the translation-based embedding method TransE, which maps the discrete symbols of entities and relationships into a continuous vector space, capturing the agent's position in the KG and enabling transitions from the current entity to the next via the selected relationship. The state of the agent in step i can be represented by the following vector:
Rewards: Select actions one by one from the head entity until reaching the real tail entity, and this action sequence is the reasoning path of the quantum policy network. Due to the large action space available to agents, there are far more incorrect action decision sequences than correct ones, and the number of incorrect decision sequences increases exponentially with the length of the reasoning path. To encourage agents to find the correct reasoning path, this paper defines the reward function of the policy network as:
Policy network: This paper trains a quantum policy function based on the quantum circuit, where represents the parameters of the quantum circuit, represents the quantum amplitude encoding of the state , and represents the probability of selecting the action in state when the parameters of the quantum circuit are . The quantum strategy network constantly interacts with the external environment, updating the parameters of the quantum circuit under the constraint of the reward function to find the optimal reasoning paths.
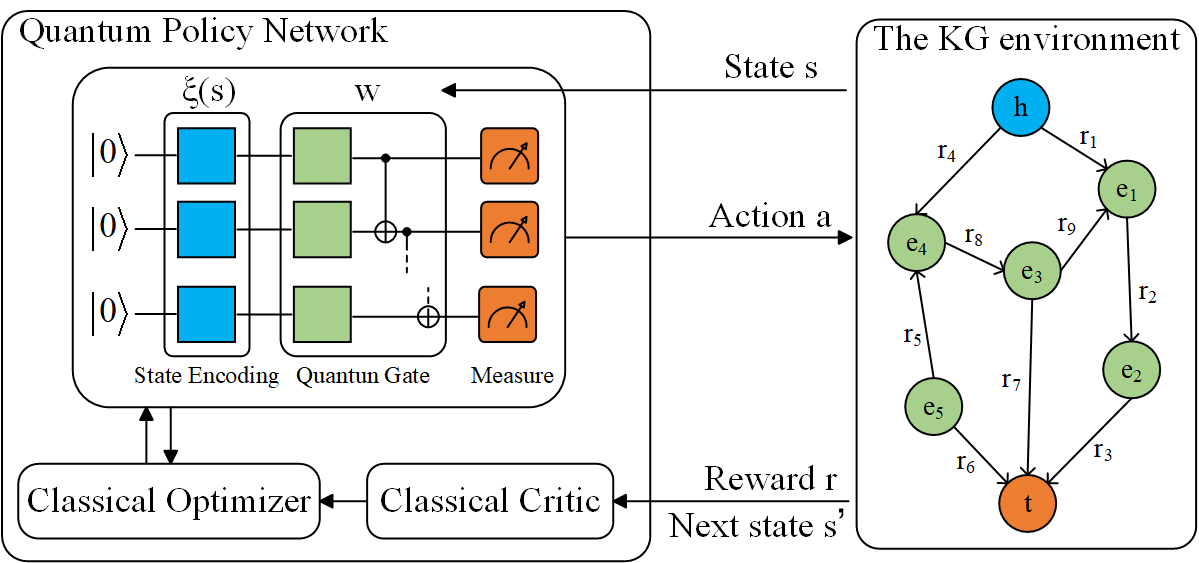
When training the policy network using the QIRL method, the current environmental state is first input into the quantum policy network and quantum encoded to initialize the input state of the quantum circuit. After quantum computing, measure the probability distribution of actions, select the action with the highest probability as the next action , and update the environmental state to . The reward function calculates the reward value based on the current environmental state and inputs it together with into the optimizer of the quantum strategy network to update the quantum circuit parameters . After training, the quantum strategy network generates reasoning paths as logical rules for entity reasoning to reason about missing entities. The flow of the QIRL method is illustrated in Figure 1.
For each entity pair , a random breadth first search (BFS) is used to find all paths between the entity pairs. This paper introduces a random mechanism in the BFS algorithm, which randomly selects an intermediate node instead of directly searching for paths between the head entity and tail entity . Then perform two BFS between and to search for the correct paths faster and improve the convergence speed of the model. For entity pairs , randomly select the inter mediate entity and perform BFS between and to find paths. Entities are usually associated with multiple different relationships. Assuming that the head entity connected to the new entity through the relationship , and then connected to the entity through the relationship , a reasoning path is obtained. connected to the new entity through relationship , and is connected to the tail entity through relationship . Therefore, the reasoning path is . Combining the two reasoning paths together, the final reasoning path between is .
This paper conducts supervised training on the quantum policy network of QIRL method based on the paths between entity pairs searched by random BFS method. The quantum strategy network maximizes the expected cumulative reward by continuously updating the parameters of the quantum circuit . The expected cumulative reward is expressed as follows:
where represents the reward value obtained by selecting action in state . For each supervised path, the agent receives a reward of +1 for each successful search and updates the quantum circuit parameters using the approximate gradient of the Monte Carlo strategy gradient:
where belongs to path , which represents the action with the highest probability of the quantum circuit output in step .
In the pretraining process of the quantum strategy network mentioned above, the reasoning paths obtained often contain a large amount of redundant information and similar paths. To improve reasoning efficiency, this paper retrains the quantum policy network using a reward function to find a more efficient reasoning path controlled by the reward function. For each entity pair , the agent selects an action from the head entity based on the output value of the quantum policy function to expand the reasoning paths. If the selected action cannot connect to any entity, the agent receives a negative reward and remains in its original state. Since agents follow the quantum policy function to extend the reasoning paths, they will not get stuck due to repeating incorrect steps. This paper improves training efficiency by limiting the maximum length of the reasoning paths. If the agent finds the correct tail entity within the maximum path length, a new reasoning path is generated. Conversely, if the agent fails to locate the correct tail entity within the constrained path length, the current training iteration is terminated. The gradient function of the quantum strategy network during the retraining process is as follows:
The retraining process of the model is shown in Algorithm 1, where is the parameters of the quantum circuit, is the quantum amplitude encoding of the input state , and represents the set of negative steps.
Entity reasoning refers to reasoning about missing entity information from known entities and their relationships through the relationships or attributes between entities in a KG. Due to the large number of complex relationships between entities in KGs, conducting path searches one by one will result in high time costs. The bidirectional path constrained search algorithm [18] is an efficient path search algorithm that can simultaneously search for paths from both positive and negative directions, significantly reducing the number of search paths. Therefore, this paper adopts a bidirectional path constrained search algorithm to search for paths between entity pairs, significantly reducing the search space and improving the efficiency of path search.
For an entity pair , the reasoning path trained by the QIRL method is used as a logical formula, starting from the head entity and tail entity respectively, and gradually expanding the reasoning paths through a bidirectional path constraint search algorithm. If the intersection of the path entities in both directions of the bidirectional path constraint search algorithm is not empty, the true tail entity can be successfully found based on the reasoning path . Otherwise, the tail entity cannot be successfully reasoned.
Data:
for episode < do
Initialize state vector
Initialize episode length
encode with Amplitude Encoding
while steps < max length do
Probability distribution of action ;
Observe reward , next state ;
if then
Save to
end if
if success or steps=max length then
then Break
end if
end while
Increase steps
Update using
reasoning Path
Assuming there is a reasoning path , perform bidirectional path constraint search on entity pair . Starting from the head entity and connecting to the entity through relationship , the forward entity collection is . At this point, if the length of the forward entity set is 1 and the length of the reverse entity set is 0, the next step is to expand . Starting from the tail entity and connecting to the entity through relationship , , at this point, the intersection of and is not empty, the tail entity is successfully reasoned out.
Quantum circuit is mainly composed of three parts: quantum bits, quantum gates, and measurements. Quantum bits exhibit unique quantum advantages compared to classical bits due to their properties of superposition states. Quantum amplitude coding is an efficient method for mapping classical data to quantum states. It encodes states with dimensions into amplitude values of quantum bits, achieving compressed representation of high-dimensional input data. The number of quantum bits in a quantum circuit depends on the dimensions of the state and action space of the KG. Assuming that the state space dimension is and the action space dimension is , the number of quantum bits needs to satisfy:
Quantum gate is the fundamental unit that operates on qubits, achieving entangled states between qubits by linearly transforming their states, and establishing complex connections between multiple qubits. CNOT gates are commonly used to generate entangled states between quantum bits, achieving parallelism in quantum computing. After passing through the CNOT gate, the quantum bits of the input circuit are rotated through the Rot gate to achieve precise control over the state of the quantum bits. The Rot gate in quantum circuit manipulates a three-dimensional weight vector to achieve rotation of quantum bits in three dimensions. Therefore, the parameter number of each layer of the Rot gate in quantum circuit is:
if the number of layers in a quantum circuit is , the parameter number of the entire quantum circuit's Rot gate, denoted as ,is:
for each quantum circuit, if a bias vector is set as , the parameter number of the bias term is:
the parameter number of the entire quantum circuit , can be expressed as:
DeepPath [18] is trained on a reinforcement learning network, which consists of two hidden layers and one output layer. Assuming that the state space dimension , the action space dimension , and the dimension of the first hidden layer is 512, the total number of parameters from input to the first hidden layer is:
the dimension of the second hidden layer is 1024, so the total number of parameters from the first hidden layer to the second hidden layer is:
the total number of parameters from the second hidden layer to the output layer is:
the total number of parameters for the DeepPath network is:
The NCRL [24] is trained based on a neural network that includes an Embedding layer, an LSTM layer, a Linear layer, and an Attention layer. Assuming the action space dimension is 16 and the Embedding layer dimension is 1024, the number of parameters in the Embedding layer is:
the parameters of the LSTM layer include the weights and biases for the input-to-hidden and hidden-to-hidden connections. Assuming both the input and hidden layer dimensions are 1024, the number of parameters in the LSTM layer is:
assuming the input and output dimensions of the Linear layer are both 1024, the number of parameters can be expressed as:
the Attention layer consists of three Linear layers, so the number of parameters in the Attention layer can be expressed as:
therefore, the total number of parameters in the NCRL model is:
Under the same parameter settings, the number of parameters required for quantum circuit is , significantly reducing the number of parameters needed for model training.
Quantum circuits, through quantum superposition and entanglement, can represent high-dimensional states with a small number of qubits. However, this compression capability has not been fully realized in current classical-based quantum simulators, where the storage and computational demands far exceed those required for actual operation on quantum hardware [27]. Classical simulators need to explicitly store the entire quantum state vector, i.e., all amplitudes [26], whereas in actual quantum hardware, these values are implicitly encoded in the physical system and do not require explicit storage. Furthermore, classical simulators cannot achieve exponential parallelism via quantum superposition states as quantum hardware can, and thus must simulate all possible paths sequentially, increasing the processing time requirement.
In this section, we first introduce the experimental setup, including the dataset, baseline, evaluation metrics, and parameter settings. Then, the main results of the proposed model were introduced, and all baselines were compared on two benchmark datasets. Furthermore, the training parameter quantities of different models were analyzed and compared.
To evaluate the performance of the QIRL method in entity prediction tasks, partial KG data was extracted from two benchmark datasets, Kinship and YAGO3-10, for testing. The Kinship dataset is small but logically complex, testing the model's reasoning ability with sparse data. The YAGO3-10 dataset is large and diverse, evaluating the model's scalability and generalization.The increase in the number of relationships in knowledge reasoning enhances the completeness of reasoning paths and improves the accuracy of knowledge reasoning. Constrained by the computational hardware's processing capabilities, the quantum reinforcement learning model in this paper contains 16 qubits and can handle 16 relationships in the dataset. To find the reasoning path more efficiently, breadth first search is performed from both the head entity and tail entity directions. The action space includes the relationships between entities and their inverse relationships. The statistical data of the extracted dataset is shown in Table 1:
| Dataset | entities | rel | train | Test | valid |
|---|---|---|---|---|---|
| Kinship | 104 | 16 | 4897 | 1226 | 581 |
| YAGO3-10 | 123183 | 16 | 313569 | 3867 | 3572 |
The QIRL model parameters proposed in this paper include the quantum bit count of the quantum circuit, the learning rate of the model training, the entity embedding dimension , the reinforcement learning discount rate , the maximum number of attempted steps for reasoning path search , etc., where num_qubits is the number of relationships contained in the dataset. To improve the generalization ability and accuracy of the model, this paper generates positive and negative samples of the test set data based on pra [25]. This paper uses a TransE based method to train embedding vector representations of entities and relationships. The optimal parameters for the model are , and .
This paper compares embedding-based methods and path-based methods to explore their performance on the dataset used in this paper. Embedding-based methods include translation-based method TransE [11], rotation-based method RotalE [19] and complex vector space-based method CompleEx [20]. Path-based methods include neural network-based and logical reasoning combined method NeuralLP [21], deep learning-based and relational reasoning combined method DRUM [22], rule-based method RulE [23], neural network-based and symbolic reasoning combined method NCRL [24], and reinforcement learning-based method DeepPath [18]. In order to ensure the fairness of the experiment., this paper used the publicly released source code of each model and adopted the best hyperparameters provided in the original text for the experiment.
| Dataset | Average Path number |
|---|---|
| Kinship | 69 |
| YAGO3-10 | 5 |
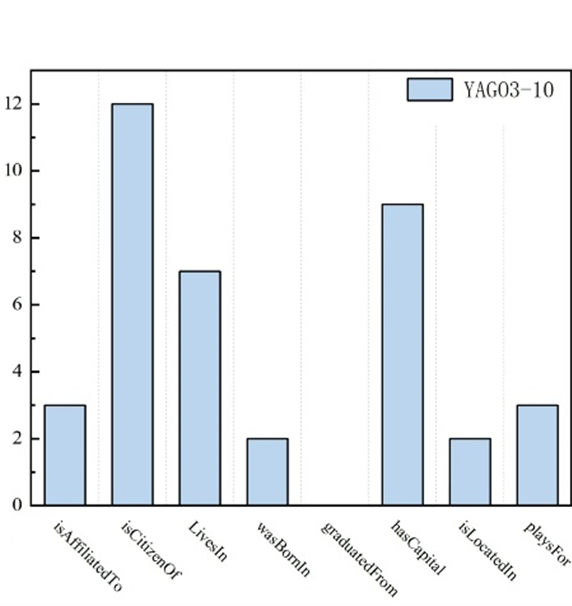
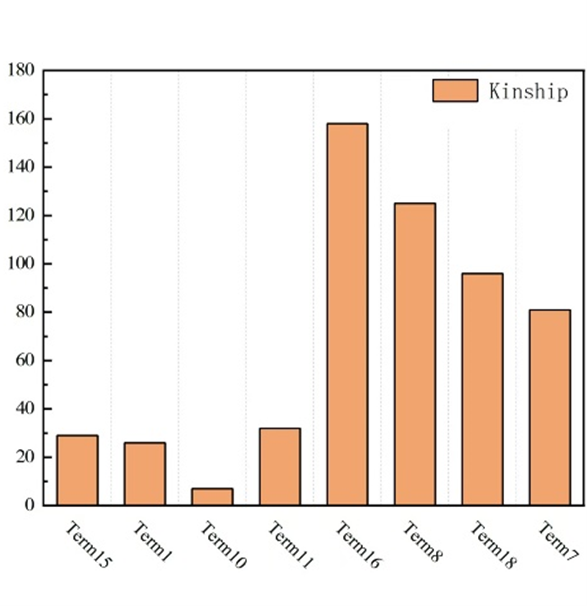
In this experiment, Mean Average Precision (MAP) and Accuracy were used as evaluation metrics. This paper primarily focuses on the tail reasoning task and evaluates it on the tail entity reasoning task, namely predicting the entity represented by in . For each test triplet , start from the head entity and search for the tail entity based on the generated reasoning paths. Tail reasoning tasks are the main focus of this paper, while head reasoning tasks and relationship reasoning tasks can also be converted into this paradigm.
Figure 2 shows the entity reasoning MAP values of the QIRL method on different relationships between the Kinship and YAGO3-10 datasets, and Table 2 lists the number of reasoning paths found by the QIRL method on the Kinship and YAGO3-10 datasets. The agent found more reasoning paths in the Kinship dataset than in the YAGO3-10 dataset, which means the agent can find strongly correlated reasoning paths in the YAGO3-10 dataset and filter out similar or unrelated ones, but it is difficult to find the most relevant reasoning paths in the Kinship dataset. In addition, when the number of reasoning paths is too small, it is also difficult to find sufficient reasoning evidence to obtain reasoning results.
As shown in Table 3, the test results of QIRL method on YAGO3-10 are better than those on Kinship, because the correlation between entities in Kinship is low, and QIRL cannot find sufficient reasoning evidence on Kinship. However, in YAGO3-10, the correlation between entities is high and the QIRL method can find sufficient reasoning evidence for reasoning, thus obtaining good test results.
| Model | Kinship | YAGO3-10 | ||
|---|---|---|---|---|
| MAP | Accuracy | MAP | Accuracy | |
| TransE[11] | 0.325 | 0.237 | 0.072 | 0.099 |
| RotalE[19] | 0.875 | 0.744 | 0.071 | 0.082 |
| ComplEx[20] | 0.806 | 0.651 | 0.041 | 0.051 |
| NCRL[24] | 0.366 | 0.337 | 0.950 | 0.950 |
| NeuralLP[21] | - | 0.088 | - | 0.001 |
| DRUM[22] | - | 0.135 | - | 0.004 |
| RulE[23] | 0.665 | 0.649 | 0.713 | 0.697 |
| DeepPath[18] | 0.307 | 0.314 | 0.658 | 0.594 |
| QIRL | 0.326 | 0.312 | 0.661 | 0.594 |
| Model | Parameter number |
|---|---|
| QIRL | 160 |
| DeepPath | 644624 |
| NeuralLP | 139936 |
| DRUM | 204513 |
| RulE | 4722205 |
| NCRL | 11564033 |
| Model | Kinship | YAGO3-10 |
|
Parameter number Improvement | ||||
|---|---|---|---|---|---|---|---|---|
| MAP | Accuracy | MAP | Accuracy | |||||
| DeepPath[18] | 0.314 | - | 0.594 | - | 644624 | - | ||
| NeuralLP[21] | 0.088 | -71.975% | 0.001 | -99.832% | 139936 | +78.292% | ||
| DRUM[22] | 0.135 | -57.006% | 0.004 | -99.327% | 204513 | +68.274% | ||
| NCRL[24] | 0.337 | 7.325% | 0.950 | 59.33% | 11564033 | -1693.919% | ||
| RulE[23] | 0.649 | 106.688% | 0.697 | 17.340% | 4722205 | -632.552% | ||
| QIRL | 0.326 | -0.637% | 0.594 | - | 160 | +99.975% | ||
Compared with embedding-based methods, path-based methods such as QIRL perform worse on Kinship. Embedding-based methods are reasoning through distance or similarity measures. The relationships in Kinship are mostly simple and symmetrical, and most relationships can be directly learned through geometric relationships in the embedding space. However, path-based methods such as QIRL do not fully utilize the simple structures in the data, so embedding-based models can better leverage their advantages. On YAGO3-10, the performance of embedding-based methods significantly decreases due to the complexity of YAGO3-10 relationship reasoning tasks. At this point, path-based methods such as QIRL can better capture the complex relationships between entities.
The performance of QIRL on Kinship and YAGO3-10 is inferior to path-based methods such as RulE and NCRL. RulE learns explicit logical rules for reasoning and directly utilizes the inherent structure and relationships in the data. Therefore, it can achieve better results on Kinship dataset with clear regularity in relationships. NCRL combines neural networks and logical reasoning, using graph neural networks to process graph structured data, which can effectively learn potential patterns between entities and relationships. Therefore, it can achieve good results in the YAGO3-10 dataset with complex relationships and no clear rules.
Table 4 shows the number of network training parameters for different models. Through comparative analysis, it can be clearly seen that compared to other methods, the QIRL algorithm requires significantly fewer parameters in the model training process, only requiring hundreds of parameters to effectively train the model and achieve excellent results. This feature enables the QIRL algorithm to significantly reduce the computational resource consumption of the model while maintaining efficient training. By significantly reducing the number of parameters, QIRL not only demonstrates significant advantages in memory and computing resources, but also effectively avoids problems such as overfitting, thereby improving the model's generalization ability and robustness in practical applications. Overall, the QIRL algorithm has improved model performance and significantly enhanced computational efficiency by optimizing the number of parameters, demonstrating its potential in complex tasks.
As shown in Table 5, QIRL significantly reduces the number of model parameter while maintaining high model accuracy. In contrast, other methods typically increase the training parameters to improve accuracy or sacrifice model accuracy in order to reduce the number of parameter. Table 5 compares exclusively neural network-based methods to ensure parameter computability.
This paper proposes a quantum reinforcement learning-based knowledge reasoning method, QIRL, which significantly reduces the number of model's training parameter and computational complexity by leveraging quantum advantages through the construction of a quantum circuit to train the policy network. However, most quantum computing still relies on classical computer simulators to test and validate quantum algorithms, and these simulators have much higher storage and computational demands compared to the actual requirements when running on quantum hardware. In the future, further optimization of the quantum reinforcement learning model's performance is expected, aiming to reduce the number of model's training parameter while improving reasoning accuracy.
 Copyright © 2025 by the Author(s). Published by Institute of Emerging and Computer Engineers. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
Copyright © 2025 by the Author(s). Published by Institute of Emerging and Computer Engineers. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. Chinese Journal of Information Fusion
ISSN: 2998-3371 (Online) | ISSN: 2998-3363 (Print)
Email: [email protected]

Portico
All published articles are preserved here permanently:
https://www.portico.org/publishers/iece/