Sustainable Energy Control and Optimization
ISSN: request pending (Online) | ISSN: request pending (Print)
Email: [email protected]


The rapid integration of distributed energy resources (DERs), such as solar photovoltaics (PV) and battery systems, fundamentally reshapes modern distribution networks. Although DERs provide environmental and economic benefits, their intermittent and decentralized nature poses significant challenges, particularly in maintaining voltage stability and ensuring grid reliability. Traditional voltage regulation equipment, such as tap changers and capacitor banks, struggles to respond effectively to the fast fluctuations caused by DERs. Consequently, smart inverter technologies equipped with advanced grid support functionalities, such as Volt/VAR control, have become critical components in modern grid operations, as endorsed by the IEEE 1547 standard [1]. Volt/VAR control enables DERs to autonomously inject or absorb reactive power based on local voltage measurements, thus contributing to real-time voltage stabilization without heavy communication requirements. While the IEEE 1547 standard defines the general structure of Volt/VAR rules, typically piecewise-linear with deadband and saturation regions, it leaves considerable flexibility to customize these control curves based on local grid conditions. Designing these curves optimally, however, is nontrivial: it involves ensuring closed-loop system stability, achieving acceptable voltage profiles, and adhering to the detailed regulatory constraints specified by IEEE 1547. Several recent studies have advanced the understanding of Volt/VAR optimization challenges. Glover et al. [2] explored centralized coordination strategies using deep reinforcement learning to control DER smart inverters dynamically, showcasing the potential of data-driven methods and highlighting the complexity of scaling traditional optimization models. Murzakhanov et al. [3] proposed a projected gradient descent-based methodology for customizing Volt/VAR rules per inverter location, focusing on maintaining voltage profiles while guaranteeing dynamic stability through convex approximations of feasible regions. Gupta et al. [4] expanded this line of research by proposing deep learning-based frameworks, wherein artificial neural networks emulate Volt/VAR dynamics, enabling efficient training of control parameters and overcoming the scaling issues of conventional optimization approaches. Other notable contributions have addressed uncertainty and robustness. Wei et al. [5] introduced a chance-constrained optimization framework to design Volt/VAR rules that minimize ohmic losses while satisfying probabilistic voltage constraints, accounting for grid variability without sacrificing operational security. Complementarily, Gupta et al. [6] examined voltage magnitude and phase imbalance issues on multiphase feeders, proposing Volt/VAR control strategies that simultaneously regulate both voltage levels and imbalance factors, further pushing the boundaries of conventional control design. Ma et al. [7] introduced the Open DER model, an open-source framework designed to accurately replicate DER behaviors defined by IEEE 1547-2018. Their model enables system planners and researchers to simulate DER interactions with the grid under various operational scenarios. Validation against laboratory-tested smart inverters demonstrated high accuracy, although some discrepancies pointed to potential areas for further model refinement. Esmaili et al. [8] developed practical optimization models for evaluating DER integration under voltage support modes to address operational issues like voltage flicker and overvoltage. Their work showed that implementing Volt/VAR and Volt/Watt functionalities can significantly reduce voltage flickers and nearly double the DER hosting capacity of distribution systems compared to constant power factor operations. Focusing on system-wide optimization, Hasan et al. [9] proposed a centralized nonlinear optimal power flow (OPF)-based method to simultaneously manage active and reactive power outputs of DERs. Tested on both IEEE 123-bus and a large 3989-bus feeder, their methodology significantly improved voltage profiles across networks with high levels of PV penetration, proving the effectiveness of centralized coordination mechanisms. In a complementary line of work, Singh et al. [10] developed a mixed-integer linear programming (MILP) approach that optimizes grid topology reconfiguration and Watt-VAR curve settings for DERs. Their results demonstrated that when coordinated with customized inverter control, dynamic reconfiguration can minimize system losses and enhance voltage regulation, particularly during rapid load changes. From a system management perspective, Stefani et al. [11] emphasized the critical role of integrating smart inverter functionalities within Advanced Distribution Management Systems (ADMS) and DER Management Systems (DERMS). Their study argued that combining local autonomous DER control with centralized system objectives transforms DERs from operational challenges into valuable grid-supporting assets. While previous work has made significant strides in tailoring Volt/VAR rules for improved grid stability and performance, challenges remain in balancing real-time adaptability, computational tractability, and full compliance with IEEE 1547 provisions. In particular, most existing solutions either oversimplify the representation of control rules, neglect certain regulatory constraints, or focus narrowly on specific feeder types without generalizing them to broader practical scenarios. In order to address these gaps, this paper develops an advanced optimization framework for designing Volt/VAR control curves customized per bus, ensuring dynamic stability, and rigorously complying with IEEE 1547 standards. Leveraging a projected gradient descent (PGD) algorithm, the proposed approach optimally adapts control curves to anticipated two-hour-ahead grid conditions, maintaining scalability and robustness even in complex, realistic distribution feeders. The framework is validated using numerical simulations on the IEEE 141-bus feeder under realistic load and solar generation scenarios, demonstrating significant improvements in voltage regulation and system resilience compared to conventional methods. The remainder of this paper is organized as follows: Section II reviews the mathematical modeling of distribution feeders and Volt/VAR rules. Section III formulates the optimization problem and presents the parameterization techniques. Section IV introduces the proposed PGD-based solution algorithm. Section V discusses simulation results and performance evaluations, and Section VI concludes the paper with a summary of contributions.
In order to effectively design control strategies for inverter-based distributed energy resources (DERs), an accurate representation of the distribution feeder is required. The feeder is modeled as a single-phase radial network consisting of buses, where bus 0 represents the substation. Let denote the vector of bus voltage magnitudes, and represents the complex power injections at each bus. The widely used linearized power flow model describes the relationship between voltages and power injections as follows:
where and are positive definite matrices reflecting the feeder topology and line impedances, is the substation voltage, and is an all-one vector. The power injections and are further decomposed into inverter-interfaced DER injections (, ) and uncontrollable loads (, ) as:
To simplify the notation, an effective reactive power injection is defined.
Thus, the voltage profile becomes:
where aggregates constant terms. This formulation highlights how the system voltages primarily depend on the reactive power support from DERs under given load and generation conditions.
The IEEE 1547 standard mandates that DERs provide reactive power support based on one of four control modes, notably voltage-dependent reactive power control (Volt/VAR). Under Volt/VAR control, inverters adjust their reactive power output as a function of local voltage deviations. The Volt/VAR curve, which is shown in Figure 1, is typically modeled as a piecewise linear function with deadband and saturation regions. Mathematically, the Volt/VAR rule can be expressed for each inverter as:
where defines the specific control curve, relating the local voltage to the inverter's reactive power output . In order to ensure stability and compliance, the slope parameters of the Volt/VAR curve must satisfy IEEE 1547 constraints, typically ensuring non-positive slopes outside the deadband and bounded saturation levels.
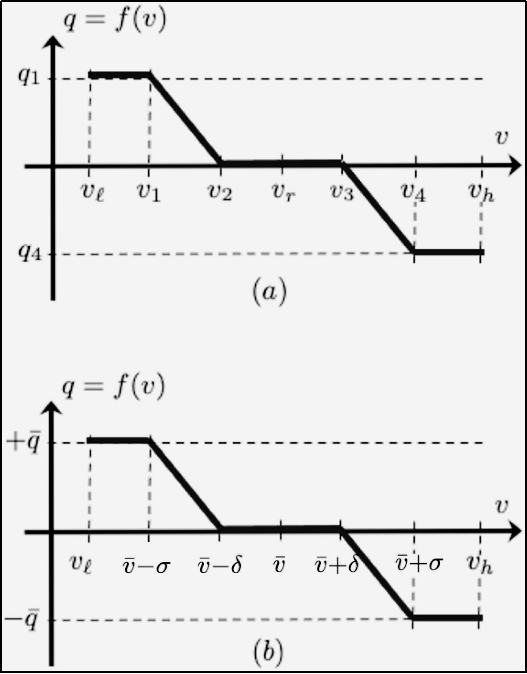
Stability analysis for networks governed by local Volt/VAR rules requires ensuring that the combined slope matrix and feeder reactance matrix satisfy the spectral norm condition:
For some small stability margin, . This ensures that the inverter dynamics converge to a stable operating point. At equilibrium, the reactive power injections satisfy:
Or equivalently:
Subject to the constraints defined by the Volt/VAR curves. Thus, the equilibrium reactive power injections can be seen as the solution to a convex optimization problem balancing voltage regulation and reactive power support, albeit based purely on local voltage information. Although this may not achieve perfect voltage uniformity, it allows for practical, autonomous DER operation without extensive communication overhead.
The problem formulation aims to design optimal Volt/VAR control rules for DERs systematically and in a scalable way. The process follows three main steps: (1) selecting a convenient parameterization of the control rules, (2) characterizing the feasible set that satisfies IEEE 1547 constraints and system stability, and (3) defining a suitable cost function to be minimized. First, a new parameter, , is introduced for each inverter to simplify the mathematical representation of the Volt/VAR curve parameters. By reparameterizing the control curves in terms of , the feasible region becomes convex, making the optimization tractable. Second, the feasible set is defined by enforcing physical limits on the control curve slopes, dead bands, and saturation points while guaranteeing dynamic stability through spectral norm constraints on the system matrices. Finally, the optimization objective is formulated to minimize voltage deviations across the feeder. Specifically, the sum of squared differences between actual voltages and the nominal value (1 pu) is minimized. This ensures that the resulting Volt/VAR rules improve voltage regulation while remaining compliant with standards and system dynamics. Furthermore, the formulation is extended to support non-symmetric Volt/VAR curves, which relax the symmetry assumption around the nominal voltage and allow for even more flexible inverter behavior without compromising stability [12, 13].
The optimal Volt/VAR rule design problem formulated earlier is inherently non-convex due to its bilevel structure: the outer optimization minimizes voltage deviations, while the inner problem determines the inverter reactive power injections based on local Volt/VAR responses. Directly solving this bilevel problem would require heavy mixed-integer programming, which is computationally expensive. In order to overcome this, the solution adopts a projected gradient descent (PGD) approach. In each iteration, the method updates the Volt/VAR parameters by moving in the direction of the negative gradient of the cost function while projecting the updates back into the feasible region defined by IEEE 1547 constraints and stability conditions. The key steps involve:
Computing the projection onto the feasible set, formulated as a second-order cone program (SOCP)
Evaluating the gradient of the voltage deviation cost function with respect to the Volt/VAR rule parameters
Using chain rule expansions to handle the dependency between voltage profiles and reactive power injections through the Volt/VAR dynamics
Updating the parameters iteratively until convergence
In order to handle the nonlinearity introduced by the piecewise-linear nature of Volt/VAR curves, careful differentiation strategies are applied, and special attention is given when the operating voltage lies within the deadband. Overall, the PGD method offers a practical and scalable way to tune Volt/VAR control rules for each inverter, balancing optimal voltage regulation performance with computational efficiency [3].
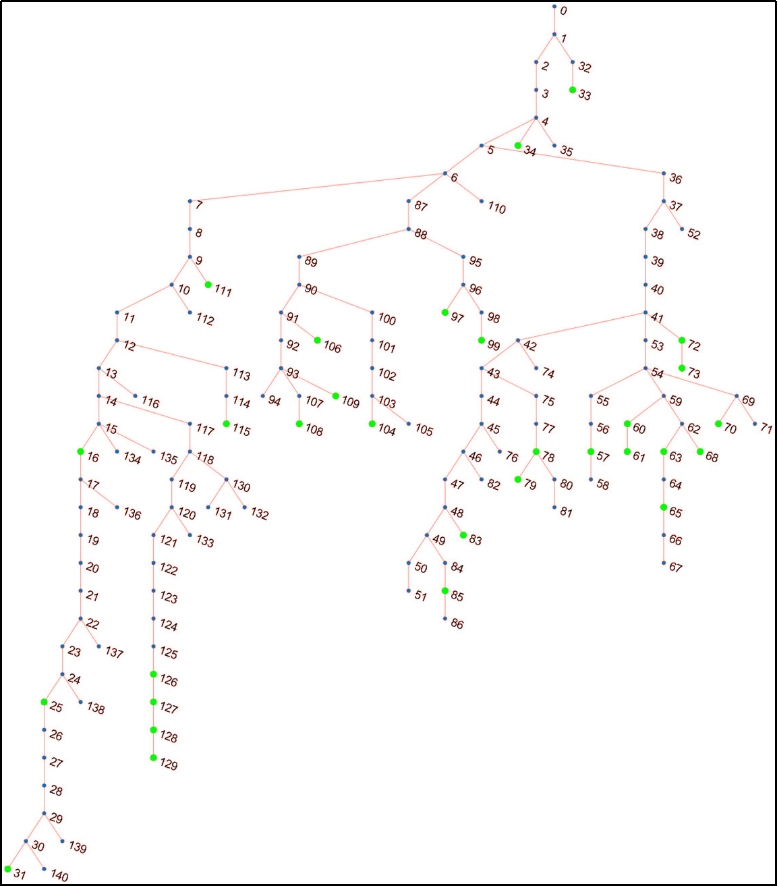
The performance of the proposed Volt/VAR control design was validated through numerical experiments on a modified version of the IEEE 141-bus distribution feeder, adapted to a single-phase configuration [14]. As the original system lacked solar installations, additional distributed generation: twenty-six photovoltaic (PV) systems rated at 0.5 MW each, and four larger 2 MW PV systems at buses 126, 127, 128, and 129 are considered, which are shown in Figure 2. All simulations were performed on a computer with an Intel(R) Pentium(R) Silver N5000 CPU operating at 1.10 GHz, 8 GB of RAM, and a 64-bit Windows 11 Enterprise system. Software tools used included MATLAB 2022a. Data from homes numbered 20 to 369 were utilized. Each of the 84 non-zero injection buses in the IEEE 141-bus system was assigned a load based on the average active power of every four consecutive homes. The active loads were scaled, ensuring the peak load per bus reached 2.5 times the benchmark system value. Reactive loads were synthetically generated by applying the IEEE 141-bus benchmark power factors. For PV generation, active power values were scaled to align the maximum production per PV unit with its benchmark rating. Volt/VAR control rules were specifically designed based on operating conditions from two distinct periods: 09:00–11:00 and 13:30–15:30. For each window, 120 one-minute samples were aggregated into 5-minute intervals, yielding representative scenarios for the optimization process. The optimal Volt/VAR parameters were determined using the Projected Gradient Descent algorithm.
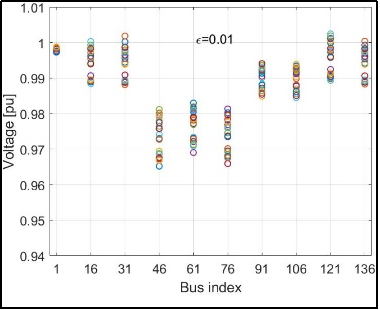
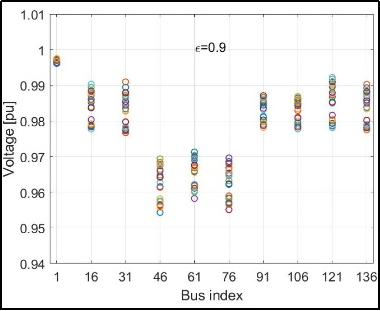
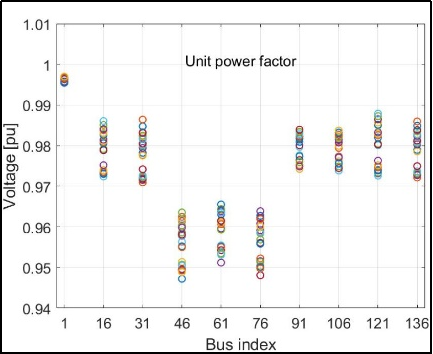
The simulation results demonstrate that implementing optimized Volt/VAR rules significantly improves voltage regulation across the feeder (Figure 3). Compared to baseline operation with inverters set at unit power factor (i.e., no reactive power support), the optimized control strategy substantially reduces voltage deviations. Without reactive support, the system experienced voltage violations exceeding the allowable range at several buses and under multiple operating scenarios. Introducing Volt/VAR rules mitigated these violations and maintained voltage profiles closer to nominal values across all tested scenarios.
An important part of the evaluation involved examining the influence of the stability margin on system performance. Simulations showed that a smaller value of achieved tighter voltage regulation than a larger margin like , albeit at the cost of a slightly more aggressive control action (Figure 3). These observations confirm the trade-off between voltage regulation quality and system stability margin, as enforced by the feasible control design set.
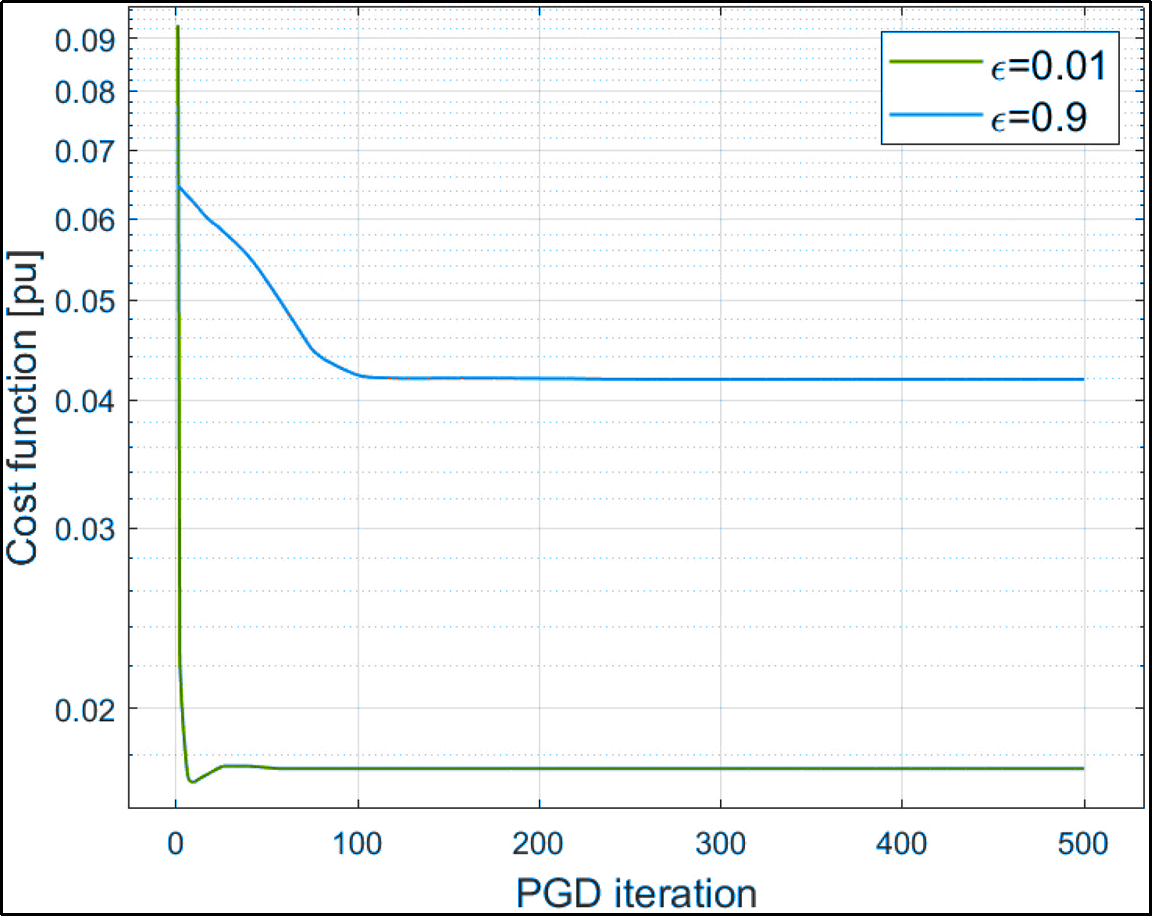
The convergence of the Projected Gradient Descent (PGD) algorithm used for optimizing the Volt/VAR rules was also analyzed, as shown in Figure 4. The cost function exhibited a smooth and consistent decrease across iterations, ensuring reliable convergence to near-optimal control settings. The convergence behavior was similar across both morning (09:00–11:00) and afternoon (13:30–15:30) operating periods, validating the robustness of the PGD method under varying load and generation conditions.
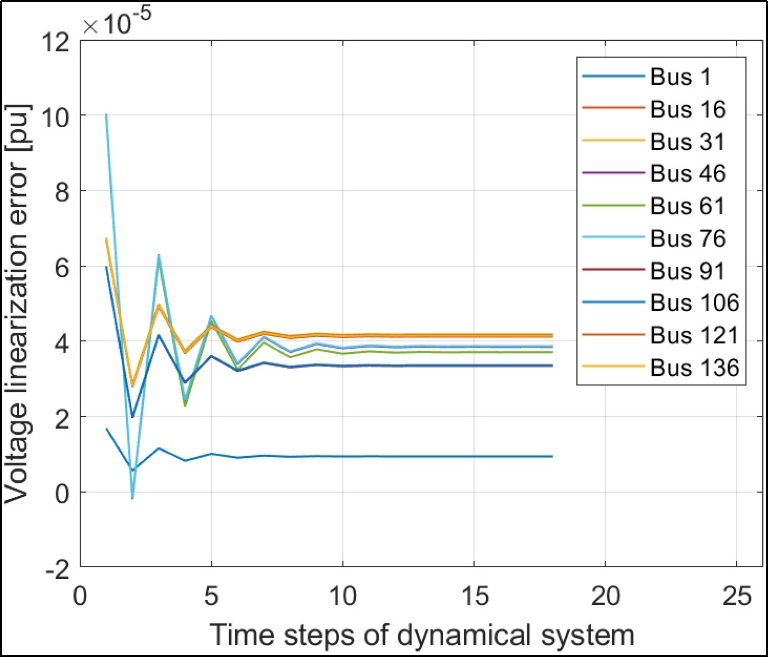
Another set of tests examined how quickly the feeder voltages settled into equilibrium after a disturbance or control update, as illustrated in Figure 5. Results indicated that voltage dynamics stabilized within a few seconds after implementing the optimized Volt/VAR curves, with minimal oscillations or overshoots. Comparisons between different feeder buses showed uniform behavior, highlighting the method's effectiveness in managing the network's real-time dynamics.
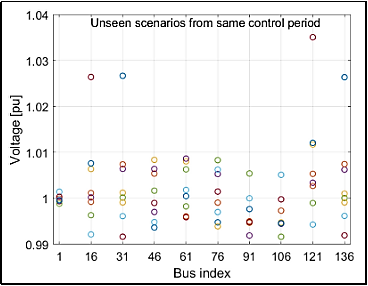
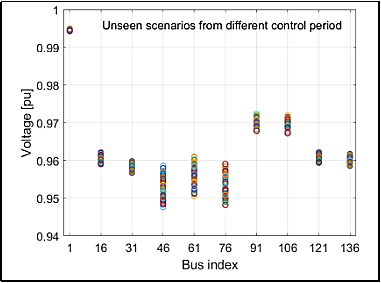
In order to test the generalization capability of the designed control rules, additional simulations were performed on unseen operating conditions not included in the training set. The optimized Volt/VAR curves maintained excellent voltage regulation even under these unforeseen scenarios, demonstrating the robustness and adaptability of the proposed approach. This performance was notably better than simple default rule settings, which suffered larger voltage deviations when facing unexpected variations. Figure 6 demonstrates this statement.
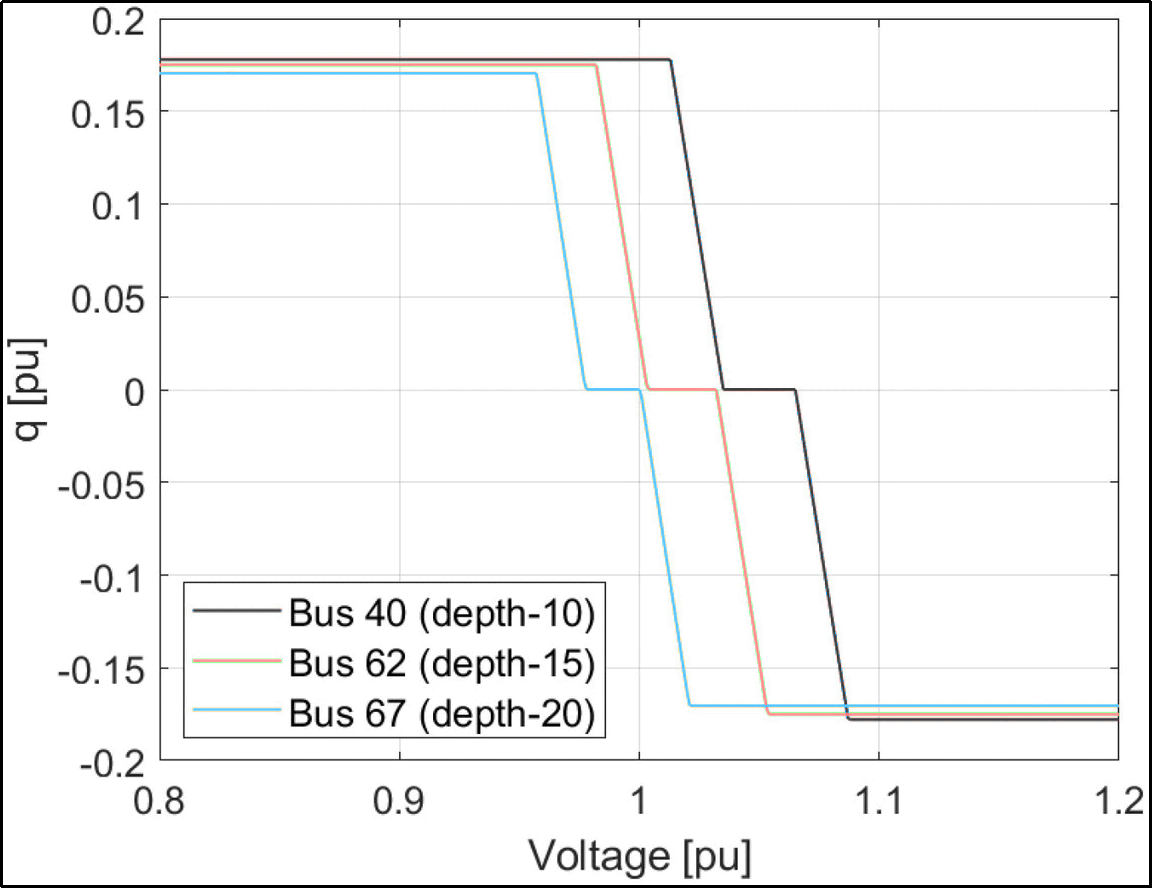
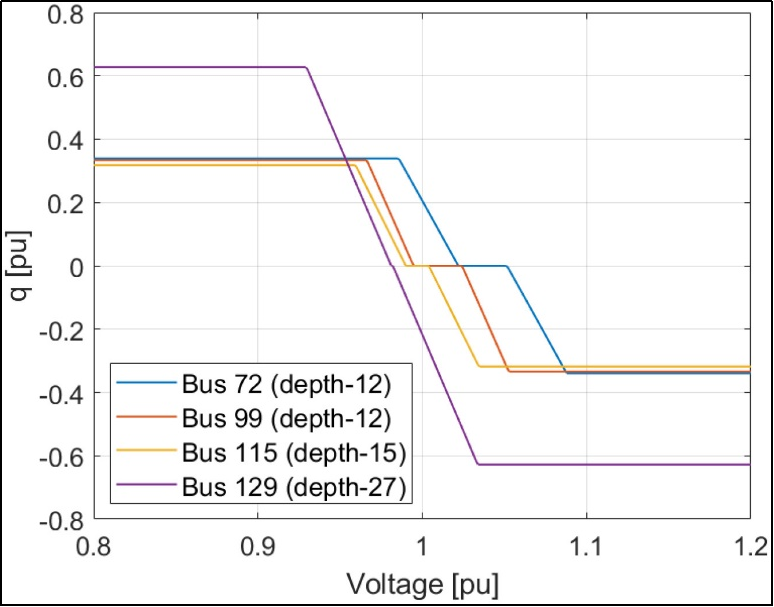
Finally, Figures 7 and 8 explored the influence of inverter locations and depths within the network. Inverters closer to the substation (smaller electrical depth) exhibited steeper Volt/VAR curves, allowing them to react more strongly to voltage deviations. In contrast, inverters farther from the substation operated with shallower curves due to their smaller influence on overall voltage regulation. These results suggest that customizing the Volt/VAR slope based on inverter position enhances control effectiveness without unnecessarily stressing remote devices.
This paper presented a scalable optimization framework for designing customized Volt/VAR control rules for inverter-interfaced DERs in single-phase distribution systems. By leveraging a projected gradient descent approach, the proposed method systematically tunes inverter control parameters to balance voltage regulation performance with dynamic system stability while fully adhering to IEEE 1547 requirements. Through extensive numerical evaluations on a modified IEEE 141-bus feeder, the approach's effectiveness was demonstrated under realistic load and solar generation conditions. The results confirmed that optimized Volt/VAR rules significantly enhance voltage profiles, reduce voltage violations, and maintain robust stability even when tested under unseen operating scenarios. The framework's flexibility also allowed tailored control settings based on inverter locations and feeder topology, further improving system-wide performance. The proposed design delivers superior voltage regulation with minimal additional computational burden compared to default standards and conventional unit power factor operations. The ability to dynamically adapt Volt/VAR curves based on forecasted grid conditions offers a practical solution for real-world distribution networks with high DER penetration. Future work may explore extending the framework to multiphase systems, incorporating real-time data-driven adjustments, and integrating coordination strategies with centralized distribution management systems to enhance grid resilience and operational flexibility further.
 Copyright © 2025 by the Author(s). Published by Institute of Emerging and Computer Engineers. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
Copyright © 2025 by the Author(s). Published by Institute of Emerging and Computer Engineers. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. Sustainable Energy Control and Optimization
ISSN: request pending (Online) | ISSN: request pending (Print)
Email: [email protected]

Portico
All published articles are preserved here permanently:
https://www.portico.org/publishers/iece/