1. Introduction

In recent years, fractional-order systems (FOSs) have become a prominent area of research and application due to their ability to model complex dynamic behaviors with greater accuracy and flexibility compared to traditional integer-order systems. The inclusion of fractional derivatives and integrals in these systems allows for the representation of memory and hereditary effects, which are crucial for accurately describing a wide range of physical, biological, and engineering processes. Additionally, FOSs offer an extensive stability region, providing enhanced robustness and control design flexibility. This broader stability region enables FOSs to maintain desired performance under varying conditions, such as external disturbances and model uncertainties, where integer-order systems often fall short. These advantages have led to widespread adoption of fractional-order models in diverse fields, including financial systems [1], diseases [2] batteries [3, 4, 5] and energy systems [6, 7].

Comparing to integer-order systems, fractional-order (FO) state-space representation offers greater flexibility and accuracy in describing a wide range of natural phenomena. However, designing controllers for FOSs presents inherent challenges due to their complex nature. Despite this, numerous research efforts have successfully advanced effective control techniques, making substantial contributions to the field, including the design of robust controllers optimal control strategies, and adaptive control techniques tailored to FOSs. In particular, in [8], a neural state estimator design was proposed for controlling chaotic FOSs. In [9], active control and unidirectional coupling were used to synchronize three-dimensional FOSs, effectively suppressing chaotic behaviour. Reference [10] examines the analysis and control of hyperchaotic financial systems modelled with FOs. In [11], synchronization of two chaotic FOSs was achieved by employing a FO sliding mode technique with a time-varying switching surface controller. Additionally, in [12, 13], an observer-based FO sliding mode control design was proposed to stabilize a practical system. In [14], a terminal sliding mode controller was developed for stabilizing an FOS, with transformation of the "sgn" function into the fractional derivatives of the controller input to achieve a chattering-free controller. Finally, in [15, 16], the author investigated the conditions for synchronizing chaotic FOSs through the activation feedback approach.

The use of fuzzy systems for modelling nonlinear systems and the development of fuzzy-based control techniques have been extensively explored in previous researches, with applications to practical systems such as satellite attitude control [17], autonomous underwater vehicles [18], power systems [19], and robotic applications [20]. For instance; an adaptive fuzzy control (AFC) is designed for tracking the trajectory of a low-scale unmanned aerial vehicle, based on a new fuzzy adaptive neural proportional integral derivative controller [21], an adaptive fuzzy tire cornering stiffness strategy and a trajectory tracking autonomous steering control strategy were proposed in [22], an adaptive fuzzy control problem is studied in [23] for a connected automated vehicles platoon subject to unknown dead-zone input and constraints and [24] studies the AFC control problem of uncertain nonlinear systems with unknown multiple classes of actuator faults.

Nonetheless, there has been limited research on using Adaptive fuzzy-based methods to control FO dynamics. For instance, in [25], a command filtered AFC approach was developed for nonlinear FOSs (NFOSs), utilizing the fractional backstepping control method. Additionally, in [26], a novel event-triggered AFC tracking approach was studied for NFOSs considering the uncertainties of the model and in presence of external disturbances. In [27], an event-triggered hybrid AFC method was proposed for a class of uncertain non-strict-feedback multi-input multi-output (MIMO) NFOSs. Finally, in [28], a fuzzy dead-zone input was used to address the tracking control of strict feedback NFOSs with unmeasurable states. These investigations reflect continuous efforts to advance effective techniques to control FOSs, which have significant potential for applications in various fields of engineering and science. Particularly, the studies underscored the use of fuzzy-based methods for managing FO dynamics, offering significant prospects for engineering and scientific applications.

This paper presents a novel method for chaos suppression of nonaffine NFOSs, which involves an FO AFC approach. The contributions of the paper are presented as follows:

This article is structured into multiple sections. Section 2 offers a survey to the fundamental concepts and preliminaries of fractional calculus and also introduces the fuzzy systems. Section 3 introduces a novel control strategy based on a FO AFC and also presents the conditions for stability of closed loop system through the fractional Lyapunov method. To validate the capability of the proposed technique, several numerical simulations are conducted on Arneodo chaotic FOS using Python in Section 4. Finally, the work is concluded in Section 5.

2. Preliminaries

2.1 Fractional Calculus

This section introduces FOSs that enables a more precise depiction of complex phenomena and real-world application comparing with integer-order model. Fractional calculus utilizes novel operators for differentiation, which can be defined as follows [29, 30]:

where $a$ and $t$ represent the integral lower and upper bounds, while $\beta$ represents the order of fractional differentiation that must meet the condition $0.5\le \left|\beta \right|\le 1$. In fractional calculus, the Caputo fractional derivative is a commonly utilized definition that generalizes differentiation to non-integer orders. It is defined by considering the function integer-order derivative and multiplying it by the gamma function of the order of the derivative. This definition is commonly employed in a range of applications as it facilitates the modelling of systems that exhibit memory and non-locality.

$$D_t^{\beta }{}_a{}^{C}f\left(t\right)=\frac{1}{\Gamma \left(1-\beta \right)}{\int }_a^t{\left(t-\tau \right)}^{-\beta }f\left(\tau \right)𝑑\tau$$

where $\Gamma$ represents the Gamma function. The Caputo fractional derivative is often considered advantageous over other fractional derivative definitions—such as the Riemann-Liouville fractional derivative—because it incorporates a memory effect that is more natural and interpretable in many physical and engineering systems.

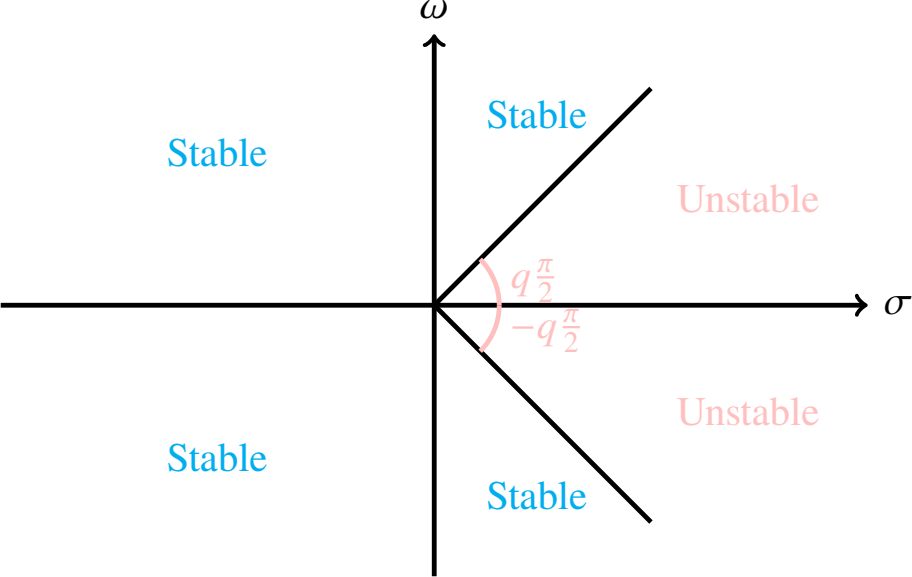
Remark 1. Consider a linear fractional order system as $D_t^{\beta }x\left(t\right)=Ax\left(t\right)$. By satisfying the condition $\left|\arg \left(\text{eig}\left(A-bK\right)\right)\right|>\beta \frac{\pi }{2}$, all the system state trajectories converge to 0. Considering , the stability of linear fractional-order systems can be illustrated in Figure 1[31, 32]. Unlike integer-order systems, fractional-order systems exhibit a broader stability region in the complex plane due to the nature of fractional derivatives, which allow for a more gradual decay of system states. This broader stability region enables fractional-order systems to tolerate larger variations in system parameters and initial conditions while maintaining stability, making them more robust in real-world applications.

Figure 1 The stability interval of commensurate linear fractional-order system with order $q$.

Lemma 1. As stated in [33, 34], let $x\left(t\right)\in {ℝ}^n$ represent a vector of differentiable functions. According to the results presented in these references, the following equation holds for any time instant $t\ge t_0$:

$D_t^{\beta }{}_a{}^C\left(x{\left(t\right)}^{T}Px\left(t\right)\right)\le \left(x{\left(t\right)}^{T}PD_t^{\beta }{}_a{}^{C}x\left(t\right)\right),$

$\forall \beta \in (0,1),\forall t\ge t_0$

where $P$ denotes a symmetric positive definite matrix. The above Lemma holds if $P$ is symmetric positive definite or positive semi-definite.

Lemma 2. As described in [35, 36], let $x\left(t\right)\in {ℝ}^n$ be a vector of differentiable functions. Then, if a continuous function $V:[t_0,\infty )\times {ℝ}^n\to ℝ$ satisfies the following condition:

$$D_t^{\beta }{}_{t_0}{}^{C}V(t,x\left(t\right))\le -\alpha V(t,x\left(t\right))$$

then:

$$V(t,x\left(t\right))\le V(t_0,x\left(t_0\right))E_{\beta }\left(-\alpha {\left(t-t_0\right)}^{\beta }\right)$$

The proof of Lemma (2) is accessible in [37] and [38].

3. Fractional Fuzzy Adaptive Controller

This section presents an innovative FO AFC designed specifically for FOSs, featuring a unique fractional update law that enhances the controller's robustness for FOSs. Fuzzy systems are effective in approximating nonlinear functions with a satisfactory degree of accuracy, which makes them a proper approach for addressing the nonlinearities inherent in chaotic FOSs. Let's express the dynamics of a non-affine NFOS as follows:

Figure 2 Fractional adaptive fuzzy controller structure.

where , $x\in {ℝ}^n$ are the states of the NFOS and $f(x,u)$ represents a smooth unmodeled function exhibiting uncertain nonlinear characteristics. Additionally, $d\left(t\right)$ is a bounded disturbance. The objective is to develop an appropriate controller that satisfies ${lim}_{t\to \infty }\Vert e\left(t\right)\Vert =0$. The configuration of the FOS in eq. (11) can be defined by the following equation:

where the matrices $A$ and $b$ can be extracted as below:

Assumption 2. To facilitate the analysis, we make the assumption that the function $f_u(x,u)=\frac{\partial f(x,u)}{\partial u}$ satisfies the following conditions, without loss of generality:

In most physical systems, the output signals are continuous by nature. For example, in mechanical systems, the position of a moving object or the velocity of a motor will change smoothly over time, without abrupt jumps or discontinuities. These assumptions simplify the analysis and are aligned with how real systems behave in practice.

Assumption 3. As outlined in [26], we assume that the target trajectory $x_d$ and all its fractional derivatives are smooth and bounded within specified limits.

Assumption 4. As stated in [43, 27], it is assumed that the disturbance is constrained within a specific bound:

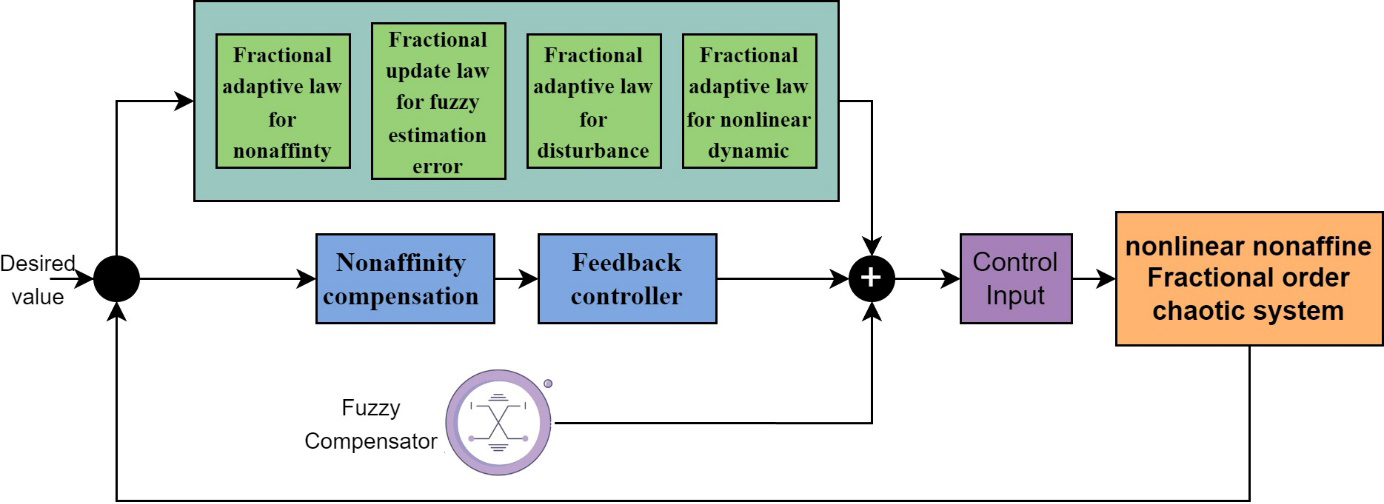
Figure 2 illustrates the structure of the proposed AFC designed to ensure stability in chaotic FOSs. In order to meet the control objective, it is essential to derive the error vector. By stabilizing the dynamics of the error, the system's states can be guided to converge to the desired trajectory.

where the error vector represented by $e$, quantifies the deviation between the system states and the target trajectory. Taking fractional derivation from eq. (16) , we can derive the dynamic of the error as follows:

By using a similar method as in eq. (12), we can express the error system as follows:

To design the controller, we introduce the variable v which can be defined as follows:

The adaptive term $v^{\prime }$ will be presented later in this paper. In order to achieve the stability of the controller, we choose the vector $K$ so that it satisfies the inequality below:

According to Assumption (2), the following inequality can be satisfied:

Applying the theorem of implicit function, it is clear that the nonlinear algebraic equation $f(x,u)-v=0$ is solvable locally for the input $u$ given any arbitrary value of $(x,v)$. Consequently, there exists an ideal controller $u^{\ast }$, that fulfills the following equality for a specified value of $(x,v)\in {ℝ}^n\times ℝ$:

By applying the mean value theorem [44, 45], we can identify a constant $\lambda$ within the interval of , such that the function $f(x,u)$ can be expressed around $u^{\ast }$ as follows:

where $f_u={\frac{\partial f(x,u)}{\partial u}|}_{u=u^{\ast }}$ and $u_{\lambda }=\lambda u+\left(1-\lambda \right)u^{\ast }$. So that eq. (18) can be rewritten as:

This paper introduces a methodology for constructing an AFC capable of estimating an ideal controller so that the ideal controller can be extracted as follows:

where ${\gamma }^{\ast }$ is the ideal parameter vector which can be defined as:

The actual controller can be defined as:

where ${\gamma }^T\psi (x,v)$ estimates the ideal controller provided in eq. (25), $u_r$ mitigates the effects of external disturbances, and ${\hat{v}}^{\prime }$ is an estimation of $v^{\prime }$. By employing these approximations, the error dynamics outlined in eq. (24) can be revised as follows:

and the following inequality is always satisfied if $P,Q>0$:

Additionally, the subsequent adaptive update laws for FOSs can be established:

Theorem 1. Considering the FO differential equations governing the error dynamics described in Equation (29) for the non-affine NFOS (11), which adheres to Assumption (2) and is subject to bounded disturbances as specified in Assumption (4), along with a desired trajectory that complies with Assumption (3), the controller input defined in Equations (27) and (28), using fuzzy rules that align with Assumption (1) and the fractional update laws outlined in Equations (31), (32), (33), and (34), will lead to the error converging to zero. This convergence occurs in a manner that fulfills the conditions of Lemma (2) and successfully satisfies the control objective ${lim}_{t\to \infty }\Vert e\left(t\right)\Vert =0$.

Proof. Let us examine the Lyapunov function defined as follows:

where ${\tilde{u}}_r=u_r-d_{\text{max}},{\tilde{u}}_{\delta }=u_{\delta }-{\delta }_{\text{max}},{\tilde{v}}^{\prime }=v^{\prime }-{\hat{v}}^{\prime }$, and $\tilde{\gamma }=\gamma -{\gamma }^{\ast }$. Taking fractional derivation based on the conditions of lemma (1) and lemma (2) gives:

after substituting the error dynamic from eq. (29) into eq. (37), we obtain:

By utilizing the control inputs specified in eq. (27) and eq. (28), the following equation is obtained:

Finally, by applying the fractional update algorithms presented in Equations (31) through (34), we derive the following inequality:

The extended Lyapunov theorem for FOSs leads to stability of the closed-loop system, and thus the tracking error converges to neighborhood of zero. Additionally, the boundedness of the coefficient parameters is guaranteed, completing the proof.

4. Simulation Results

In this section, we will demonstrate the application of the FO AFC to the FO Arneodo chaotic system. The simulations for this study were conducted using Python, leveraging its robust numerical computing libraries for implementing the proposed fractional-order adaptive fuzzy controller. The fractional-order Arneodo chaotic system was modeled using the Caputo definition of fractional derivatives, ensuring an accurate representation of system memory effects. Numerical solutions to the fractional-order differential equations were obtained using the Cputo approximation, which is widely regarded for its accuracy and stability in fractional-order computations. To achieve reproducibility, the following parameter settings were used: the step size for numerical integration was set to h=0.01, and the fractional-order q was fixed at 0.9 for the Arneodo system. Gaussian membership functions were utilized for the fuzzy controller as detailed in Section 3. The simulation environment was implemented on a standard computing platform with an AMD R7 7840H processor and 32GB of RAM.

The FO Arneodo system extends the classical Arneodo chaotic system, which consists of a three-dimensional set of ordinary differential equations characterized by nonlinear dynamics. This fractional version includes a fractional derivative term that captures the memory effect within the system, offering a more precise representation of real-world systems that display long-term memory behaviour. The system is defined by three nonlinear differential equations, where the fractional derivative is taken with respect to the Caputo sense. To begin, we provide the dynamical model of the Arneodo chaotic FOS as follows:

where, $a=5.5$, $b=3.5$, $r=0.4$, and $q=0.9$. The simulations conducted in previous investigations have provided valuable insights into the behavior of the FO Arneodo system under different orders of fractional derivations. The findings of these simulations indicate that chaos can exist in the system for orders less than 3, with chaotic attractors and phase portraits observable when $q$ is set to 0.9, 0.8, and 0.7. However, no chaotic behavior is observed when $q$ is set to 0.6 or 0.5, suggesting that the system's lowest limit of fractional order $q$ for chaos to occur is 0.7. In our simulations, we follow these conditions and set $q$ to 0.9 to demonstrate the efficacy of the designed controller in suppressing the chaotic behavior of the system.

To ensure optimal performance of the proposed adaptive fuzzy controller, careful selection of the adaptive parameters is essential. In this study, we provide a detailed guideline for choosing these parameters, focusing on two key aspects: adaptive gain tuning and the initialization of parameter values. The adaptive gains, denoted as ${\zeta }_1$, ${\zeta }_2$, ${\zeta }_3$, and ${\zeta }_4$, play a critical role in adjusting the controller's response to changes in system dynamics, and its value must be carefully tuned to balance fast convergence with stability. For instance, we initially set ${\zeta }_1=0.3$, ${\zeta }_2=0.7$, ${\zeta }_3=2.3$, and ${\zeta }_4=3.5$ based on prior knowledge of the system's behavior and adjusted it iteratively during simulations, with values ranging between 0.1 and 10, depending on the performance observed. Additionally, the initialization of the controller's parameters is crucial for ensuring that the system starts with an appropriate operating point. We initialized the parameters of the fuzzy system, including the membership function scaling factors, based on the expected dynamics of the Arneodo chaotic system, to achieve optimal tracking performance. The initial values for the fractional derivations are $\left[0.4-\mathrm{0.2\; 0.3}\right]$ and the adaptive parameters are set as $f_{\text{min}}=2$, ${\zeta }_1=10$, ${\zeta }_2=10$, ${\zeta }_3=20$, and ${\zeta }_4=30$. Moreover, $d\left(t\right)=2\sin \left(\pi t\right)$ and we consider using Gaussian membership functions to design a fuzzy controller for chaos suppression of FO Arneodo system.

Figure 3 First state of fractional Arneodo system with control action for time greater than 10 seconds. (Left: sgn(.), Right: tanh(.)).

Figure 4 Second state of fractional Arneodo system with control action for time greater than 10 seconds. (Left: sgn(.), Right: tanh(.)) .

Figure 5 Third state of fractional Arneodo system with control action for time greater than 10 seconds. (Left: sgn(.), Right: tanh(.)).

Figure 6 Chaotic attractor of fractional Arneodo system which is stopped its chaotic behaviour in time greater than 10 seconds. (Left: sgn(.), Right: tanh(.)).

Figure 7 Control Input (Left: sgn(.), Right: tanh(.)).

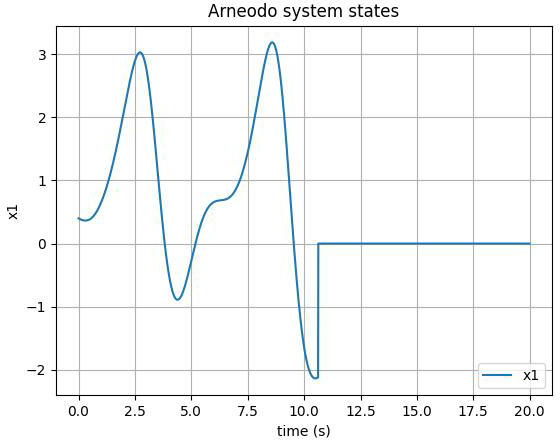
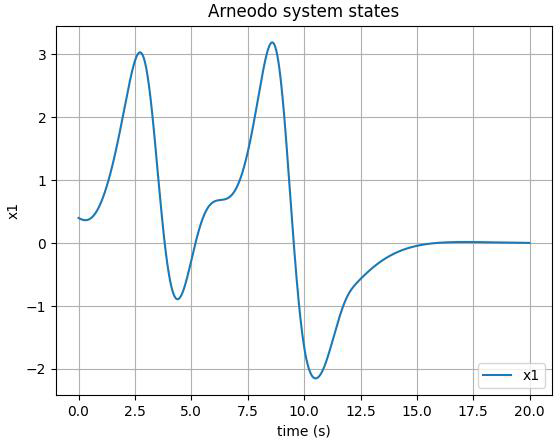
Remark 2. The control input of the system utilizes the hyperbolic tangent function, tanh(.), which presents several advantages over the traditional sign(.) function. While the sign function produces abrupt changes in control input, leading to potential instability due to rapid switching, the tanh(.) function provides a smooth transition between its values. This characteristic reduces the effects of model uncertainties and external disturbances more effectively. The continuous nature of tanh(.) helps maintain stability in system outputs and control inputs by avoiding the sharp transitions associated with the sign(.) function. In this paper, the tanh(.) function is employed as a refined approximation for the sign(.) function, enhancing the overall performance of the control strategy.

Figure 8 Comparison of settling times for the fractional Arneodo system states under different control actions (sgn(.) and tanh(.)) after 10 seconds..

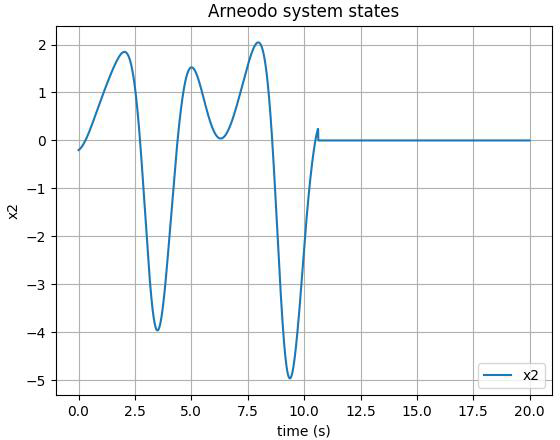
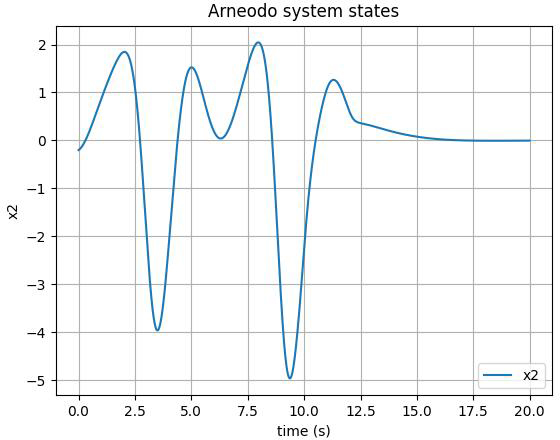
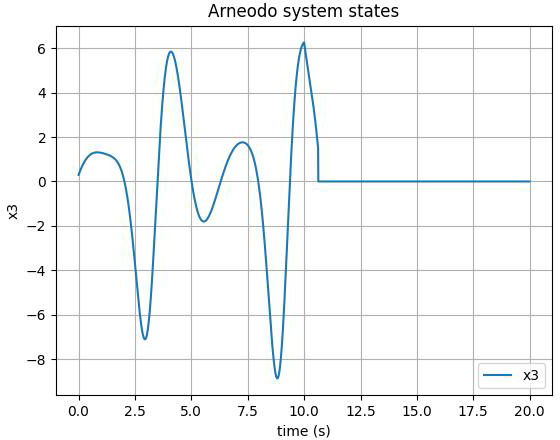
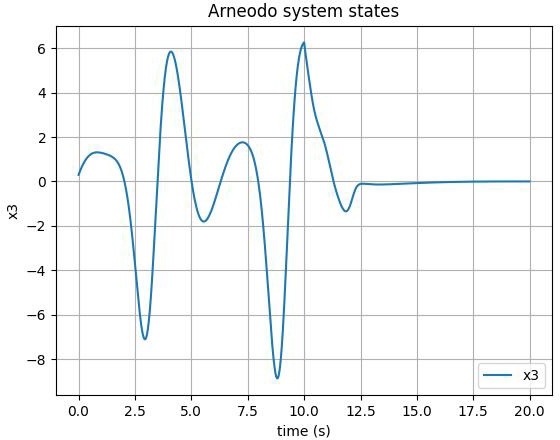
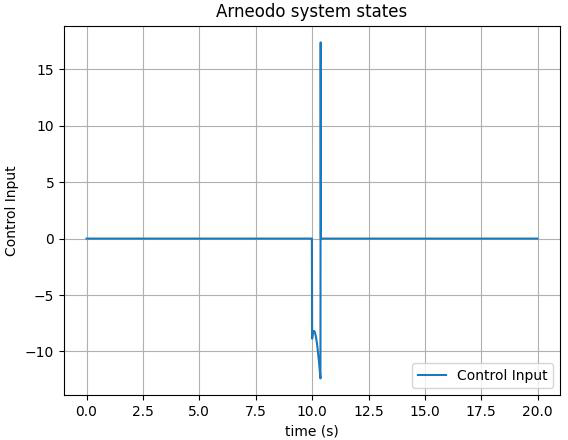
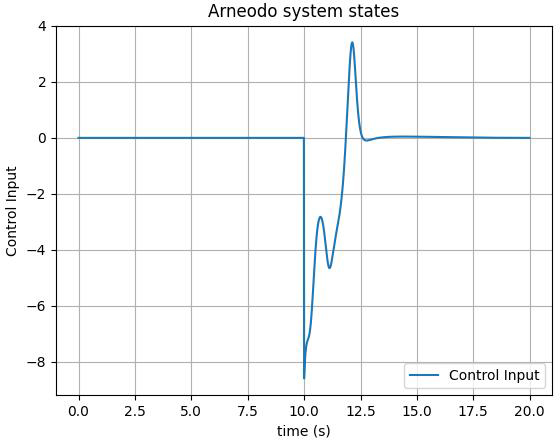
The first, second, and third state of the FOS are depicted in Figures 3-5, respectively. As illustrated, the control input is implemented on the system at t>10. The chaotic behavior can be seen in the form of unpredictable fluctuations in the state variables of the system. However, once the designed control action is applied, we can observe that the chaotic behavior of the system is effectively suppressed. The trajectory of the state variables becomes smoother and more stable, indicating that the system has been brought under control. Moreover, adding a tanh(.) function to the control input of the Arneodo system can lead to smoother control by restricting the output's rate of change and decreasing the frequency of switching so that it facilitates a more seamless and gradual shift between control actions.

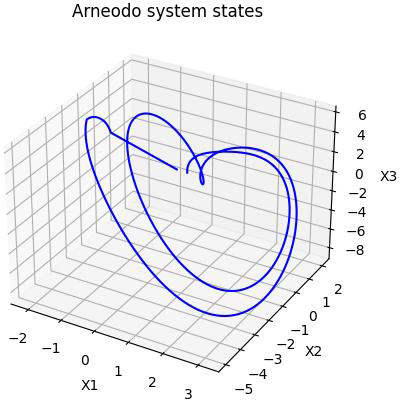
In Figure 6, It can be observed that the FO Arneodo chaotic attractor exhibiting chaotic attractor prior to the application of control action. Once the control action is implemented, the chaotic behavior is successfully suppressed and the trajectory moves straight towards zero. Moving on to Figure 7, we can observe the control input starting to suppress the chaotic behavior of the FOS at t>10. Prior to the application of the control input, the system was exhibiting chaotic behavior, as can be seen in the erratic trajectory of the state variables. However, once the control action is applied, we can see that the system starts to stabilize and converge towards a steady state. The control input acts as a stabilizing force, counteracting the destabilizing effects of the chaotic behavior and allowing the system to reach a desired state.

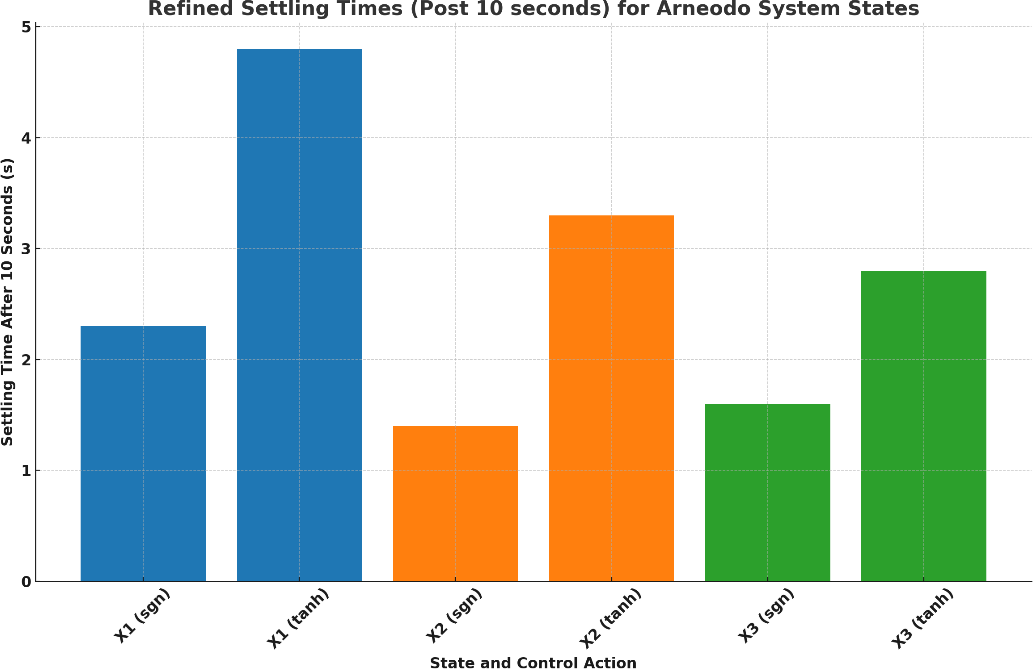
Figure 8 compares the settling times of the Arneodo system states under sgn(.) and tanh(.) control functions. Generally, it confirms that the tanh(.) function results in longer settling times across states compared to sgn(.), indicating a much smoother stabilization effect. Overall, the results demonstrate the effectiveness of the designed controller in suppressing the chaotic behavior of the Arneodo FOSs. Moreover, the hyperbolic tangent function, is used as a smooth function to reduce the switching in the control input of the Arneodo system. By applying tanh(.) to the control input, the switching frequency is reduced significantly, which improves the performance of the system and reduces wear and tear on the mechanical components in the system. Moreover, Table 1 provides a clear comparison of the key performance metrics between the tanh(.) and sign(.) functions.

Remark 3. To evaluate the efficacy of the proposed fractional-order adaptive fuzzy controller, we compare its performance with other control techniques for fractional-order chaotic systems reported in the literature. The fractional-order sliding mode control approach discussed [46, 47, 48] demonstrated robust synchronization of chaotic systems, but its reliance on time-varying switching surfaces can lead to high-frequency chattering, which is minimized in our method using the smooth tanh(.) function. Similarly, the event-triggered adaptive fuzzy control framework introduced by [49, 50, 51] showed significant reduction in control effort; however, its performance under high disturbance levels was less effective compared to our method's robust adaptation to external disturbances.

5. Conclusion

In conclusion, this paper presents an effective approach for controlling nonlinear non-affine systems with FO dynamics. The AFC technique, paired with a novel fractional update law, demonstrates robust performance by mitigating chaotic behavior and ensuring precise trajectory tracking. Simulation results on the FO Arneodo chaotic system shows the method's robustness to uncertainties, rapid error convergence, and strong disturbance rejection capabilities. The potential of the proposed fractional controller for advancing control in FOSs offers a promising direction for future studies across various applications, including robotics, power systems, biomedical engineering, and autonomous vehicles.

6. Future Directions

While the proposed adaptive fuzzy controller for fractional-order nonlinear systems demonstrates promising results in controlling chaotic behavior and tracking desired trajectories, several avenues for future research can further enhance its performance and applicability.