IECE Transactions on Advanced Fuzzy Systems
ISSN: request pending (Online) | ISSN: request pending (Print)
Email: [email protected]


Discrete multivalued logic was generalized into a continuous logic by Zadeh [1], who also introduced ordinary fuzzy sets (OFS)—the first formalization in fuzzy set theory—defined by an element and its degree of membership. In OFS, the non-membership (or non-belongingness) of an element is the complement of its membership degree to 1.
This complementary feature of ordinary fuzzy sets was criticized by various researchers. According to those researchers, the membership degree of an element should be also fuzzy and there should be no necessity for the complementary feature in OFS. Thus, by adding the fuzziness to membership degrees and/or by removing the complementary feature, OFS have been extended to several new extensions that define membership functions with more details. The extensions of OFS are historically presented in Figure 1.
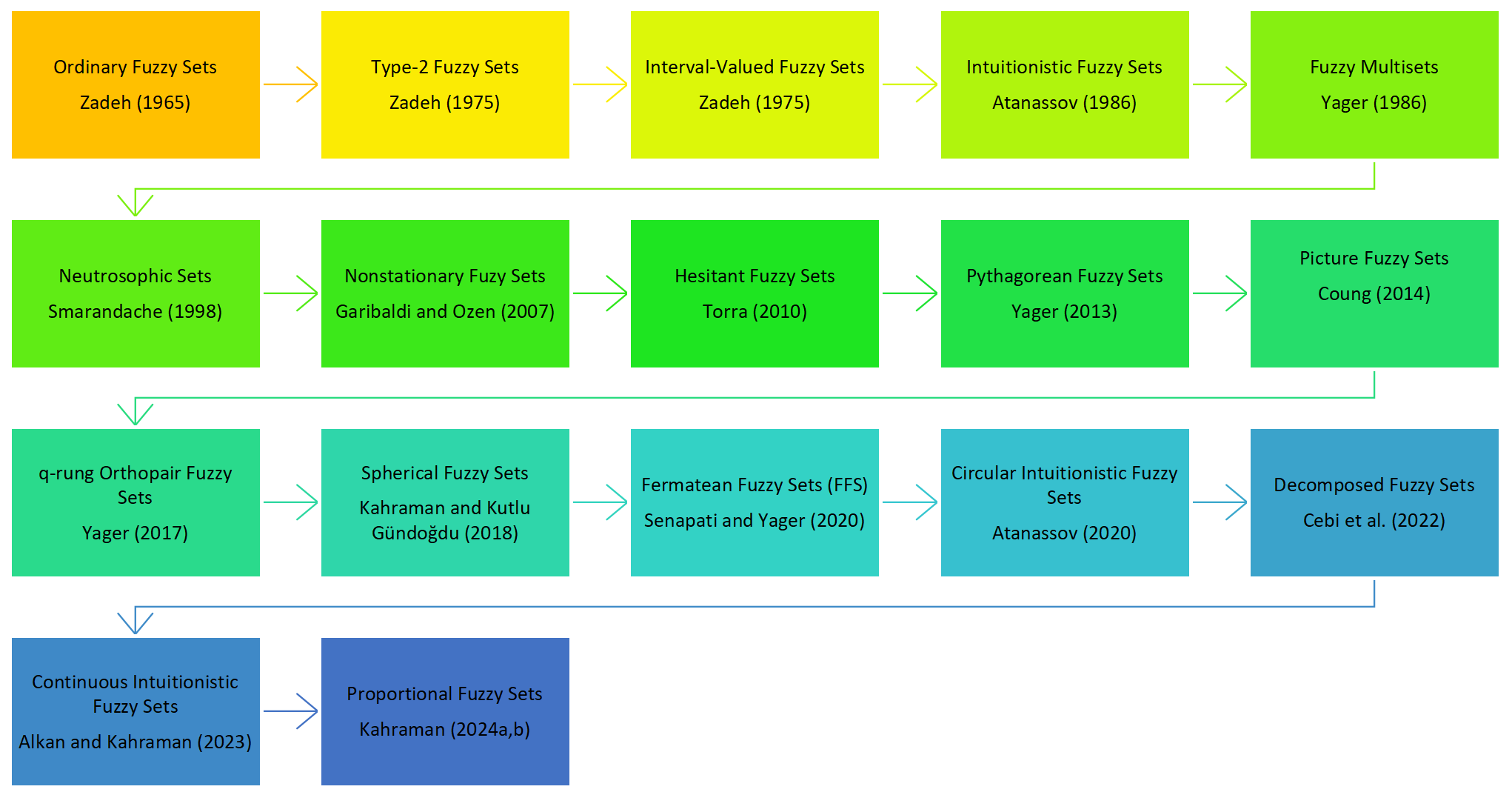
Type-2 fuzzy sets (Type-2 FS) and interval-valued fuzzy sets were developed, which let membership functions also be fuzzy by Zadeh [13]. Atanassov [2] introduced intuitionistic fuzzy sets (IFS) including elements with their degrees of membership and non-membership whose sum can be at most equal to 1. The complementary degree of the membership and non-membership degrees making the sum equal to one is called the hesitancy or indeterminacy degree of the decision maker. Torra [9] introduced hesitant fuzzy sets (HFS) to deal with a set of potential membership values of an element in a fuzzy set. Atanassov et al. [12] introduced intuitionistic type-2 fuzzy sets (IFS2) in his book, which let squared sum of membership and non-membership degrees be at most equal to one. Later, Yager [11] called IFS2 as Pythagorean fuzzy sets (PFS). Yager [10] also introduced q-rung orthopair fuzzy sets (Q-ROFS) as a generalization of IFSs, which the sum of qth powers of membership and non-membership equals at most one. Smarandache [8] introduced neutrosophic sets (NS) whose degrees of truthiness, indeterminacy, and falsity for each element in the universe can be equal to at most one and thus their sum can be at most 3. Coung [4] introduced picture fuzzy sets (PiFS) with three parameters which are called yes, no, and abstain and their complement to one as refusal degree. Kahraman et al. [7] introduced spherical fuzzy sets (SFS) which the squared sum of the same parameters as picture fuzzy sets can be at most equal to one. Later, some more recent extensions have been introduced to the literature such as circular intuitionistic fuzzy sets [2], decomposed fuzzy sets [15], continuous intuitionistic fuzzy sets [16], and proportional fuzzy sets [5, 6]. Figure 1 shows the history of ordinary fuzzy set extensions in the literature.
The goal of all of these expansions is to describe an element's membership to a fuzzy set with more parameters and information. Proportional fuzzy sets are related to determine the values of membership parameters in a more sensitive, stable and accurate way. Instead of direct assignment of membership degrees, the proportions between parameters are required from experts.
| One dimensional extensions () | Two dimensional extensions () | Three dimensional extensions () | ||||||||
| Type | OFS | TYPE-2 FS | IFS | PFS | FFS | Q-ROFS | NS | PiFS | SFS | T-SFS |
| Sum | 1 | 1 | ||||||||
| Type of sum | 1st degree | 1st degree | 1st degree | Squared sum | Cubic sum | degree sum | 1st degree | 1st degree | Squared sum | degree sum |
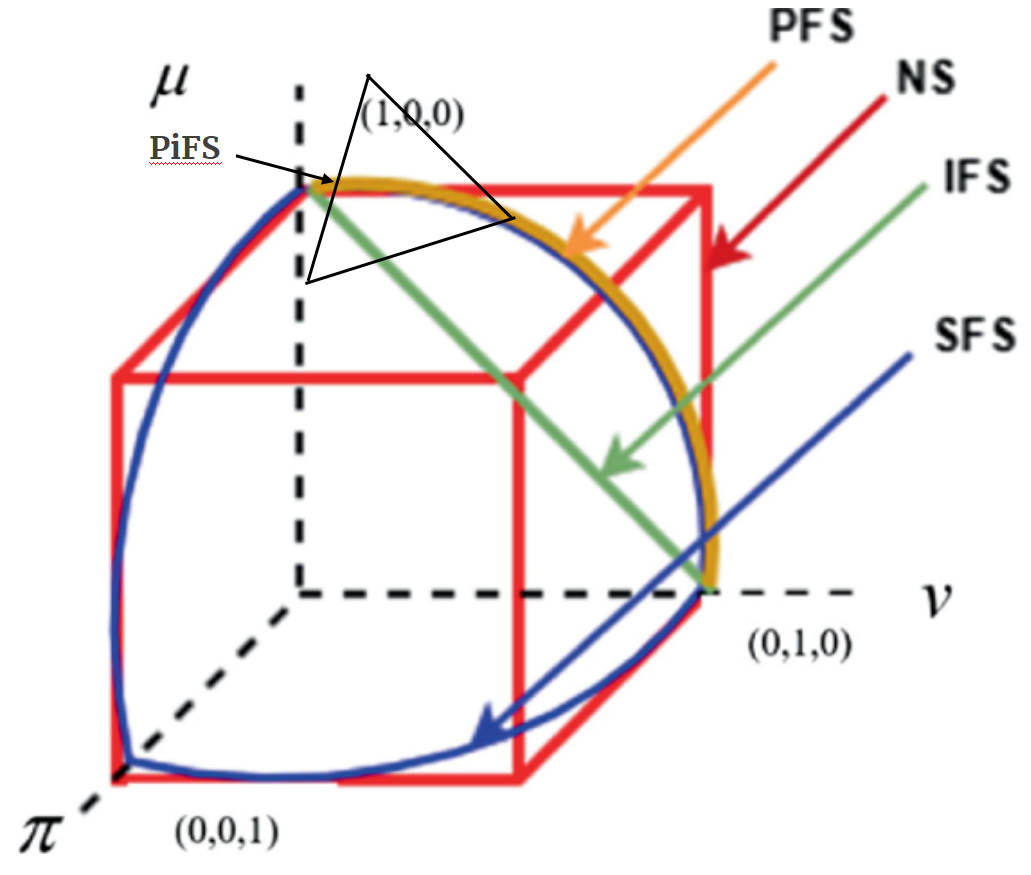
The above fuzzy sets extensions are represented by Figure 2[3]. If they are two dimensional, a surface represents the extension whereas they are three dimensional, a volume represents the extension.
Table 1 shows the extensions of OFS based on the number of parameters in their definitions. Additionally, the sum of the parameters and types of the sum operations are indicated in Table 1.
Among the fuzzy set extensions, the most popular extension is the intuitionistic fuzzy sets followed by picture and spherical fuzzy sets. Then, Pythagorean fuzzy sets and Fermatean fuzzy sets [14] follow. As the origin of the theory is based on the vagueness and impreciseness in human thoughts and perceptions, the most often used areas of fuzzy set extensions are still decision-making and fuzzy control.
It is very important that the journal in which it is published is as promising as the quality of the article. Your contributions to the field of fuzzy set theory will receive many citations in the IECE Transactions on Advanced Fuzzy Systems journal and will add value to your work. The IECE Transactions on Advanced Fuzzy Systems aims to publish high-quality research that advances the theory, methodology, and applications of fuzzy systems in various fields such as linguistic modeling, fuzzy control, fuzzy decision making, new developments and/ or innovative approaches in fuzzy set extensions. The journal will have important indexing and abstracting services soon. The journal is free of publication charges until otherwise announced. The journal is especially open to submissions on the fuzzy set extensions mentioned in Introduction section.
 Copyright © 2025 by the Author(s). Published by Institute of Emerging and Computer Engineers. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
Copyright © 2025 by the Author(s). Published by Institute of Emerging and Computer Engineers. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. IECE Transactions on Advanced Fuzzy Systems
ISSN: request pending (Online) | ISSN: request pending (Print)
Email: [email protected]

Portico
All published articles are preserved here permanently:
https://www.portico.org/publishers/iece/